Ostrosłup prawidłowy czworokątny
Otrzymałeś(aś) rozwiązanie do zamieszczonego zadania? - podziękuj autorowi rozwiązania! Kliknij
Ostrosłup prawidłowy czworokątny
Witam, mam zadanie ze stereometrii, jest ono dosyć trudne:
Treść: W ostrosłupie prawidłowym czworokątnym odległości środka wysokości od krawędzi bocznej i ściany bocznej wynoszą odpowiednio: a i b. Obliczyć objętość ostrosłupa.
Ja oznaczyłem sobie wysokość ostrosłupa jako 2x ( jej połowy wynoszą x). Krawędź podstawy jako k, a krawędź boczną jako c i wys. trójkąta równoramiennego (ściany bocznej) jako h. Utworzyłem 3 trójkąty prostokątne, z tw. pitagorasa uzyskałem 3 układy równań, z których po wyliczeniach wyszło mi, że \(k^2=16x^2\). Mamy obliczyć objętość, więc Pp*H. Wysokość= 2x, a Pp=\(k^2= 16x^2\). Teraz tylko trzeba uzależnić x od a i b, myślę, że trzeba to zrobić z dwóch trójkątów prostokątnych, które powstały po poprowadzeniu odległości od krawędzi bocznej i ściany bocznej, ale ani z własności sinusów ani z cosinów, ani z niczego innego nie mogę tego wyznaczyć, stąd moja prośba o pomoc,
dziękuję z góry
Treść: W ostrosłupie prawidłowym czworokątnym odległości środka wysokości od krawędzi bocznej i ściany bocznej wynoszą odpowiednio: a i b. Obliczyć objętość ostrosłupa.
Ja oznaczyłem sobie wysokość ostrosłupa jako 2x ( jej połowy wynoszą x). Krawędź podstawy jako k, a krawędź boczną jako c i wys. trójkąta równoramiennego (ściany bocznej) jako h. Utworzyłem 3 trójkąty prostokątne, z tw. pitagorasa uzyskałem 3 układy równań, z których po wyliczeniach wyszło mi, że \(k^2=16x^2\). Mamy obliczyć objętość, więc Pp*H. Wysokość= 2x, a Pp=\(k^2= 16x^2\). Teraz tylko trzeba uzależnić x od a i b, myślę, że trzeba to zrobić z dwóch trójkątów prostokątnych, które powstały po poprowadzeniu odległości od krawędzi bocznej i ściany bocznej, ale ani z własności sinusów ani z cosinów, ani z niczego innego nie mogę tego wyznaczyć, stąd moja prośba o pomoc,
dziękuję z góry
- anka
- Expert

- Posty: 6591
- Rejestracja: 29 sty 2009, 23:25
- Podziękowania: 31 razy
- Otrzymane podziękowania: 1119 razy
- Płeć:
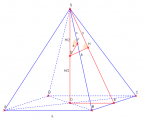
\(|FS|=x\)
\(|HS|=y\)
Z Pitagorasa dla trójkąta GFS
\((\frac{H}{2})^2=a^2+x^2\)
Z Pitagorasa dla trójkąta GHS
\((\frac{H}{2})^2=b^2+y^2\)
Stąd
\(a^2+x^2=b^2+y^2\)
Z podobieństwa trójkątów GFS i OBS
\(\frac{x}{a}=\frac{H}{\frac{k\sqrt2}{2}}\)
\(\frac{x}{a}=\frac{2H}{k\sqrt2} \Rightarrow 2H=\frac{xk\sqrt2}{a}\)
Z podobieństwa trójkątów GHS i OES
\(\frac{y}{b}=\frac{H}{\frac{k}{2}}\)
\(\frac{y}{b}=\frac{2H}{k} \Rightarrow 2H=\frac{ky}{b}\)
stąd
\(\frac{xk\sqrt2}{a}=\frac{ky}{b}\)
\(y=\frac{xb\sqrt2}{a}\)
Podstawiamy do \(a^2+x^2=b^2+y^2\) i obliczamy \(x\)
Mając \(x\) z \((\frac{H}{2})^2=a^2+x^2\) można policzyć \(H\), a potem \(k\)
Znasz odpowiedź do zadania, to ją podaj. Łatwiej będzie sprawdzić czy w rozwiązaniu zadania nie ma błędu.
- anka
- Expert

- Posty: 6591
- Rejestracja: 29 sty 2009, 23:25
- Podziękowania: 31 razy
- Otrzymane podziękowania: 1119 razy
- Płeć:
\(\frac{x}{a}=\frac{2H}{k\sqrt2}\)
Potrzebne jest \(k^2\)
\(k=\frac{aH\sqrt2}{x}\)
\(k^2=\frac{2a^2H^2}{x^2}\)
\(H=\frac{2ab}{\sqrt{2b^2-a^2}}\)
\(H^2=\frac{4a^2b^2}{2b^2-a^2}\)
\(x^2=\frac{a^2(b^2-a^2)}{a^2-2b^2}\)
Potrzebne jest \(k^2\)
\(k=\frac{aH\sqrt2}{x}\)
\(k^2=\frac{2a^2H^2}{x^2}\)
\(H=\frac{2ab}{\sqrt{2b^2-a^2}}\)
\(H^2=\frac{4a^2b^2}{2b^2-a^2}\)
\(x^2=\frac{a^2(b^2-a^2)}{a^2-2b^2}\)
Znasz odpowiedź do zadania, to ją podaj. Łatwiej będzie sprawdzić czy w rozwiązaniu zadania nie ma błędu.
