Strona 1 z 1
Oblicz stosunek pól koła
: 29 lis 2015, 14:22
autor: donquixote
Proszę o pomoc w zadaniu:
W trójkącie prostokątnym, którego najmniejszy kąt ma miarę \(\alpha\) środki mniejszej przyprostokątnej i przeciwprostokątnej należą do okręgu stycznego do przeciwprostokątnej. Oblicz stosunek pól koła ograniczone tym okręgiem i trójkąta.
: 29 lis 2015, 16:32
autor: donquixote
pomocyy

Re: Oblicz stosunek pól koła
: 29 lis 2015, 18:39
autor: Panko
Można tak , dłużyzzzna .
Wprowadzam układ współrzędnych tak ,że \(C=(0,0)\) to wierzchołek kąta prostego dla \(\Delta ACB\) , \(B=( 0,2a)\) , \(A=(2b,0)\) , wtedy \(|\angle BAC|= \alpha\)
Środek przeciwprostokątnej \(AB\) ma współrzędną : \(D=(b,a)\) . Szukany okrąg jest styczny w tym punkcie do tej przeciwprostokątnej.
Środek krótszej przyprostokątnej : \(BC\) ma współrzędną \(E=(0,a)\)
Środek \(S=(x_s,y_s)\) szukanego okręgu leży na symetralnej przeciwprostokątnej \(AB\) . Jego długość promienia to \(r\)
Ma być \(|SD|=|SE|\) a stąd \((x_s-0)^2+(y_s-a)^2=(x_s-b)^2+(y_s-a)^2\) a stąd \(x_s=-(x_s-b)\) czyli \(x_s=\frac{b}{2}\)
Teraz prosta zawierająca przeciwprostokątną to
\(y= \tg (180^ \circ - \alpha ) \cdot x+2a\) czyli \(\\)\(\\) \(y=- \tg \alpha \cdot x+2a\)
Prosta do niej prostopadła , symetralna przeciwprostokątnej , na niej leży szukany środek to \(y=\frac{1}{ \tg \alpha } \cdot x+a-\frac{b}{ \tg \alpha }\)
Czyli \(y_s=\frac{1}{ \tg \alpha } \cdot x_s+a-\frac{b}{ \tg \alpha }\) oraz \(x_s=\frac{b}{2}\) stąd
\(y_s=a-\frac{b}{2 \cdot \tg \alpha }\)
........................................................................................................
POle \(\Delta ACB\) =\(\frac{1}{2} \cdot 2a \cdot 2b=2ab\)
Pole istotnego koła =\(\pi r^2\) , gdzie np \(r^2=|SE|^2=(x_s-0)^2+(y_s-a)^2= \frac{b^2}{4} \cdot (1+\frac{1}{ \tg ^2 \alpha })\)
Potrzeba jeszcze odczytać \(\tg \alpha =\frac{2a}{2b} =\frac{a}{b}\) czyli \(a=b \cdot \tg \alpha\)
.......................................................................................................
Szukany iloraz pól \(\frac{Pole koła}{ Pole \Delta ACB}\)\(=\frac{ \pi \cdot \frac{b^2}{4} \cdot (1+\frac{1}{ \tg ^2 \alpha } )}{2ab}\)=\(=\frac{ \pi \cdot \frac{b^2}{4} \cdot (1+\frac{1}{ \tg ^2 \alpha } )}{2 \cdot b^2 \tg \alpha }\)\(=\)\(=\frac{ \frac{ \pi }{4} \cdot (1+\frac{1}{ \tg ^2 \alpha } )}{2 \cdot \tg \alpha }\)
: 29 lis 2015, 20:31
autor: donquixote
dziękuję bardzo a mógłby ktoś pomoc mi jeszcze w rysunku?
: 29 lis 2015, 20:37
autor: donquixote
szczerze mówiąc nie bardzo rozumiem
: 29 lis 2015, 20:50
autor: Panko
Niestety mam z obsługą programów graficznych i całą resztą problem.
: 29 lis 2015, 21:29
autor: radagast
Akurat mam:
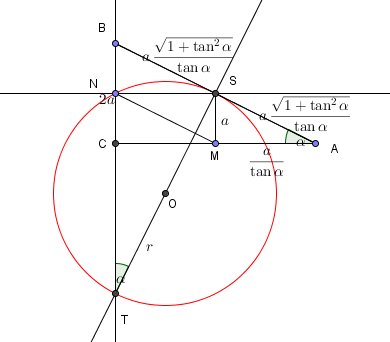
- ScreenHunter_794.jpg (14.65 KiB) Przejrzano 2012 razy
Wszystkie trójkąty prostokątne , które tu występują są podobne, więc wyznaczenie r to czysta formalność (i trochę rachunków)
