Strona 1 z 1
wykazanie nierówności
: 27 lip 2014, 09:16
autor: piteer
Pokaż ze \(\sqrt{x^4+7x^3+x^2+7x}+3\sqrt{3x}\ge10x-x^2\) w swojej dziedzinie.
: 28 lip 2014, 09:13
autor: kacper218
Jeśli prawa strona jest ujemna, to nierówność jest prawdziwa.
Jeśli prawa strona jest dodatnia to możemy podnosić do kwadratu i wtedy rozwiązywać

: 28 lip 2014, 10:05
autor: piteer
\(x^4+7x^3+x^2+7x +2\sqrt{x^4+7x^3+x^2+7x} \cdot3\sqrt{3x}+27x \ge 100x^2-20x^3+x^4\)
i co dalej?
: 28 lip 2014, 10:11
autor: radagast
Ja zaczęłabym od wyznaczenia dziedziny, potem (zgodnie ze wskazówkami kacpra) zauważysz, że należy się zająć przypadkiem \(x \in \left<0,10 \right>\) i może jakoś pójdzie.
No i oczywiście to co pod pierwiastkiem rozłóż na czynniki.
: 28 lip 2014, 10:37
autor: piteer
już podniosłem do kwadratu i co teraz z tym
Re: wykazanie nierówności
: 28 lip 2014, 12:02
autor: radagast
\(\sqrt{x^4+7x^3+x^2+7x}+3\sqrt{3x}\ge10x-x^2 \iff \\
\sqrt{x(x^2+1)(x+7)}+3\sqrt{3x}\ge x(10-x) \So x \in \left<0, \infty \right)\)
mamy już dziedzinę.
Teraz zgodnie ze wskazówkami Kacpra:
jeśli
\(10x-x^2 \le 0\) czyli
\(x \in \left(- \infty ,0 \right> \cup \left<10, \infty \right)\) to nierówność jest spełniona w sposób oczywisty.
Pozostało więc wykazać nierówność tylko dla
\(x \in \left(0,10 \right)\).
W tym celu podnieśmy obie (dodatnie) strony nierówności do kwadratu:
\(x(x^2+1)(x+7)+27x+ 6 \sqrt{3}x \sqrt{(x^2+1)(x+7)} \ge x^2(10-x)^2 \iff\)
\((x^2+1)(x+7)+27+ 6 \sqrt{3} \sqrt{(x^2+1)(x+7)} \ge x(10-x)^2 \iff\)
\(x^3+7x^2+x+34+ 6 \sqrt{3} \sqrt{(x^2+1)(x+7)} \ge 100x-20x^2+x^3 \iff\)
\(27x^2-99x+34+ 6 \sqrt{3} \sqrt{(x^2+1)(x+7)} \ge 0 \iff\)
no i to rzeczywiście liczy się dość podle

ale prawdziwe jest. Na styk, ale jest :
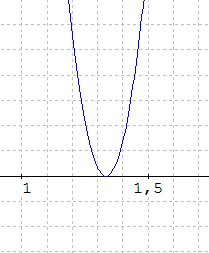
- ScreenHunter_992.jpg (11.81 KiB) Przejrzano 446 razy
Niestety, jeśli chodzi o dowód metodami tradycyjnymi wiele nie wskóraliśmy. Jak była nierówność stopnia 4 , tak jest. Myślę, że metoda Kacpra - niedobra

Re: wykazanie nierówności
: 28 lip 2014, 13:13
autor: piteer
ok dzięki wielkie
Re: wykazanie nierówności
: 28 lip 2014, 16:26
autor: Panko
Może tak .
Konieczne do wykonania grubsze rachunki : to drugie pochodne pewnych funkcji.Oraz wartości pierwszych pochodnych w pewnym punkcie.
Idea dowodu : pokazuje istnienie wspólnej stycznej do dwóch wykresów pewnych funkcji , tak że jeden jest w górnej półpłaszczyźnie a drugi w dolnej .
.....................................................................................................................
Dziedzina nierówności =\([0, \infty )\)
Dla \(\\)\(x=0\) nierówność jest prawdziwa.
Dla \(\\)\(x>0\) pomnóżmy obustronnie nierówność przez \(\frac{1}{ \sqrt{x} }\) i nieco przekształćmy i dostaniemy:
\(\sqrt{x^3+7x^2+x+7} \ge \sqrt{x} \cdot (10-x)- \sqrt{27}\)
Nazwijmy : \(f(x)= \sqrt{x^3+7x^2+x+7} ,x \in (0, \infty )\) \(\\) ,\(\\) \(g(x)= \sqrt{x} \cdot (10-x)- \sqrt{27} , x \in (0, \infty )\) i obie są w swojej dziedzinie klasy \(\\) \(C^ \infty\)
Sprawdzamy rachunkiem ( sprawdź), że \(\forall\)\(x \in (0, \infty )\)\(\\)\(f''(x)>0\) , skąd jest,że styczna do wykresu funkcji w każdym punkcie \((x_0,f(x_0) )\) gdzie \(x_0>0\) leży poniżej wykresu :
czyli \(\forall x_0>0\) \(\\) \(\forall x>0\) \(\\) \(\\)\(f(x) \ge f'(x_0) \cdot (x-x_0) +f(x_0)\).
Podobnie jest dla drugiej funkcji :
Sprawdzamy rachunkiem ( sprawdź), że \(\forall\)\(x \in (0, \infty )\)\(\\)\(g''(x)<0\) , skąd jest,że styczna do wykresu funkcji w każdym punkcie \((x_0,g(x_0) )\) gdzie \(x_0>0\) leży powyżej wykresu :
czyli \(\forall x_0>0\) \(\\) \(\forall x>0\) \(\\)\(\\) \(g(x) \le g'(x_0) \cdot (x-x_0) +g(x_0)\).
Teraz wystarczy wskazać wspólną styczną dla obu wykresów .
Faktycznie sprawdzamy rachunkiem ,że dla \(x_0=\frac{4}{3}\) jest \(f(x_0)=g(x_0)\) , oraz \(f'(x_0)=g'(x_0)\) . Czyli ta wspólna styczna która rozcina płaszczyznę tak ,że powyżej niej jest wykres \(y=f(x)\) a poniżej \(y=g(x)\) , jest wystawiana w punkcie o odciętej \(x_0=\frac{4}{3}\).
Wtedy \(x_0=\frac{4}{3}\) \(\\)\(\forall x>0\)\(\\)\(\\)\(f(x) \ge f'(x_0) \cdot (x-x_0) +f(x_0)= g'(x_0) \cdot (x-x_0) +g(x_0) \ge g(x)\)\(\\)\(\\) czyli żądana nierówność.
: 28 lip 2014, 17:45
autor: kacper218
Ja jestem ciekaw na jakim poziomie nauki jest to zadanie

Ja tego nie liczyłem, ale byłem przekonany, że jak to jest z podręcznika do lo (tutaj jest temat) to pójdzie standardowo i łatwo
