graniastosłup, ostrosłup, obwód figury

[Martynka301]

1. Podstawą graniastosłupa prostego jest romb o przekątnych długości 6 cm i 8 cm. Powierzchnia boczna graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
2. Przekrój ostrosłupa prawidłowego czworokątnego, zawierający przekątną podstawy i wierzchołek ostrosłupa jest trójkątem równoramiennym, którego pole wynosi \(12 \sqrt{3}[\tex] , a kąt przy podstawie ma miarę 30 stopni. Oblicz objętość ostrosłupa.
3. W ostrosłupie prawidłowym trójkątnym wysokość ma długość \(3 \sqrt{3}[\tex] , a krawędź podstawy ma długość 12 cm. oblicz pole powierzchni całkowitej.
4. W trapezie równoramiennym ramię ma długość 8 cm, a kąt ostry ma miarę 60 stopni. Na dłuższej podstawie zbudowano trójkąt równoboczny o boku równym tej podstawie tak, że otrzymano pięciokąt. Wiedząc, że obwód tej figury wynosi 62 cm, oblicz pole trapezu.
5. Pola dwóch podobnych prostokątów są równe 64 i 36. Jaki jest stosunek długości przekątnych tych prostokątów?\)\)

[ef39]

5
stosunek pól = kwadrat skali podobieństwa
\(k^2= \frac{64}{36}\\
k= \frac{8}{6}\)

Odpowiedź: Stosunek długości przekątnych tych prostokątów wynosi 8/6

[ef39]

4

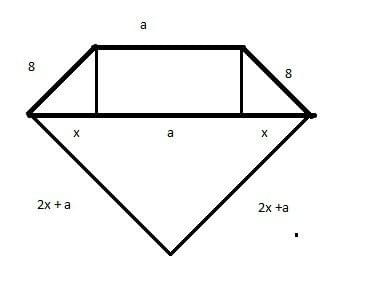
z własności trójkąta prostokątnego o kącie ostrym \(60^0\) wyznaczamy x = 4 oraz wysokość trapezu \(h=4 \sqrt{3}\)
z warunku na obwód:
\(a+8+8+2x + a +2x + a =62\\
a = 10\\\)
podstawy trapezu wynoszą 18 i 10
zatem pole trapezu wynosi
\(P= \frac{18+10}{2} \cdot 4 \sqrt{3}=56 \sqrt{3}\)

[ef39]

3


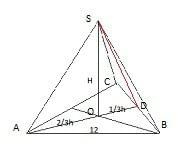
\(H=3 \sqrt{3} , a=12\\
h= \frac{12 \sqrt{3} }{2} =6 \sqrt{3}\\
|OD|= \frac{1}{3} h=2 \sqrt{3}\)
wysokość ściany bocznej |SD| policzymy przy pomocy tw. Pitagorasa
\((3 \sqrt{3})^2+(2 \sqrt{3})^2=|SD|^2\\
|SD|= \sqrt{39}\\
P_c= \frac{12^2 \sqrt{3} }{4}+3 \cdot \frac{12 \sqrt{39} }{2}= ...\)

[irena]

1.
a- bok rombu
\(a^2=3^2+4^2=9+16=25\\a=5cm\)

Wysokość graniastosłupa jest równa obwodowi podstawy

\(H=4a=4\cdot5=20cm\)

\(P_p=\frac{6\cdot8}{2}=24cm^2\\V=24\cdot20=480cm^3\)

[irena]

2.
d- przekątna kwadratu podstawy
H- wysokość ostrosłupa
b- długość krawędzi bocznej ostrosłupa

Masz trójkąt równoramienny o podstawie d i ramionach b. Wysokość tego trójkąta opuszczona na podstawę d to H.
Kąt przy podstawie ma miarę \(30^0\)

Trójkąt prostokątny o przyprostokątnych H i \(\frac{d}{2}\) oraz przeciwprostokątnej b to połowa trójkąta równobocznego, w którym H to połowa boku, a \(\frac{d}{2}\) to wysokość

\(\frac{d}{2}=H\sqrt{3}\)

Z pola tego trójkąta
\(\frac{d}{2}\cdot H=12\sqrt{3}\\H\sqrt{3}\cdot H=12\sqrt{3}\\H^2=12\\H=2\sqrt{3}cm\)

\(\frac{d}{2}=2\sqrt{3}\cdot\sqrt{3}=6\\d=12cm\)

Podstawa jest kwadratem, czyli rombem o przekątnych 12cm

\(P_p=\frac{12\cdot12}{2}=72cm^2\)

\(V=\frac{1}{3}\cdot72\cdot2\sqrt{3}=48\sqrt{3}cm^3\)