dowody z dwusieczny kątów wewnętrznych i zewnętrznych równol

[54321]

Poprowadzono dwusieczne kątów wewnętrznych i zewnętrznych równoległoboku który nie jest rombem. Udowodnij, że:
a) punkty przecięcia się tych dwusiecznych są wierzchołkami prostokątów;
b) proste zawierające przekątne tych prostokątów przechodzą przez środki boków równoległoboku;
c) długość przekątnej większego prostokąta równa się sumie długości dwóch kolejnych boków równoległoboku;
d) długość przekątnej mniejszego prostokąta równa się różnicy długości dłuższego i krótszego boku równoległoboku.

[anka]

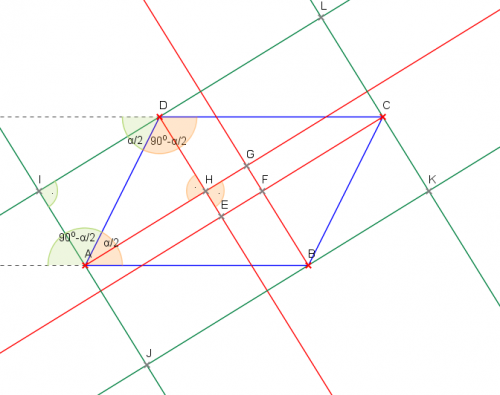
dwusieczne kątów wewnętrznych - linie czerwone
dwusieczne kątów zewnętrznych - linie zielone
\(\alpha\) - kąt ostry równoległoboku
\(180^o-\alpha\) - kąt rozwarty równoległoboku

a)
Dwusieczne kątów wewnętrznych

Trójkąt AHD
\(\angle HAD= \frac{\alpha}{2}\)
\(\angle ADH=90^o- \frac{\alpha}{2}\)
Z sumy kątów trójkąta AHD mamy:
\(\angle AHD=180^o-(\frac{\alpha}{2}+90^o-\frac{\alpha}{2}) =90^o\)

Kąty AHD i EHG są wierzchołkowe, więc są równe czyli \(\angle EHG=90^o\)
Reszta kątów podobnie, czworokąt EFGH ma wszystkie kąty proste, jest więc prostokątem.
---------------------------------------------------------------------------------------------------
Dwusieczne kątów zewnętrznych

Kąt zewnętrzny do kąta BAD jest równy \(180^o-\alpha\)
Kąt zewnętrzny do kąta ADC jest równy \(\alpha\)

Trójkąt IAD
\(\angle ADI= \frac{\alpha}{2}\)
\(\angle IAD=90^o- \frac{\alpha}{2}\)
Z sumy kątów trójkąta IAD mamy:
\(\angle AID=180^o-(\frac{\alpha}{2}+90^o-\frac{\alpha}{2}) =90^o\)
Reszta kątów podobnie, czworokąt IJKL ma wszystkie kąty proste, jest więc prostokątem.

[54321]

a mógłby mi ktoś pomóc z podpunktem b i d

[anka]

d

a1.png (16.86 KiB) Przejrzano 5562 razy

\(|\angle A'AD|= |\angle AA'D|\) - kąty naprzemianległe są równe
Trójkąt \(AA'D\) jest więc trójkątem równoramiennym.
\(|DA|=|DA'|=b\)

Wyznaczam \(|A'C|\)
\(|A'C|=|DC|-|DA'|\\
|A'C|=a-b\)

Z podpunktu b) wynika, że HF jest równoległe do DC.
Dwusieczne kątów ostrych są do siebie równooległe.
Zatem czworokąt HFCA' jest równoległobokiem, czyli
\(|HF|=|A'C|=a-b\)

na b) pomysłu brak

[54321]

może ktoś inny pomoże z tym b

[octahedron]

bgyk.png (20.22 KiB) Przejrzano 5553 razy

Pewnie jest jakiś prostszy sposób, ale ja mam taki. Trójkąty \(BCF\) i \(AHD\) są prostokątne, niech \(P\) i \(Q\) będą środkami ich przeciwprostokątnych. Środek przeciwprostokątnej jest środkiem okręgu opisanego, czyli \(|CP|=|PF|\), \(\angle CFP=\angle PCF\), stąd \(\angle FPC=180^o-2\angle PCF=180^o-\angle BCD=\angle ABC\), więc \(FP\parallel AB\). Prosta \(FP\) przechodzi więc przez \(Q\). Analogicznie wykazujemy, że prosta \(QH\) przechodzi przez \(P\), a ponieważ przez dwa punkty \(P\) i \(Q\) przechodzi tylko jedna prosta, \(F\) i \(H\) muszą oba na niej leżeć. Podobnie z trójkątów \(DEC\) i \(ABG\) dowodzimy dla drugiej przekątnej prostokąta.

[anka]

Załącznik bgyk.png nie jest już dostępny

Pewnie jest jakiś prostszy sposób, ale ja mam taki: trójkąty \(BCF\) i \(AHD\) są prostokątne, a \(P\) i \(Q\) są środkami ich przeciwprostokątnych.

Skąd to wiadomo?

A może tak:

23a.png (19.07 KiB) Przejrzano 5542 razy

Trójkąt \(AD'H\) jest podobny do trójkąta \(C'BF\) (odpowiednie kąty są sobie równe)

\(|AD'|=|C'B|=b\)

Trójkąt \(DHA'\) jest podobny do trójkąta \(B'FA\) (odpowiednie kąty są sobie równe)

\(|DA'|=|B'C|=b\)
wynika stąd, że wszystkie te trójkąty są przystające.

Wysokości poprowadzone odpowiednio z punktów H i F muszą więc być równe, czyli leżeć na prostej wyznaczonej przez punkty przechodzące przez połowę wysokości równoległoboku (a zatem równoległej do boku równoległoboku)
----------------------
Albo jakoś wykorzystać fakt, że H leży w połowie boku DD' (AH jest wysokością trójkąta równoramiennego AD'D),
a F leży w połowie boku BB' (CF jest wysokością trójkąta równoramiennego B'BC)

[octahedron]

bgyk.png

Pewnie jest jakiś prostszy sposób, ale ja mam taki: trójkąty \(BCF\) i \(AHD\) są prostokątne, a \(P\) i \(Q\) są środkami ich przeciwprostokątnych.

Skąd to wiadomo?

Z równości kątów wierzchołkowych - kąty czworokąta \(EFGH\) są proste.

[anka]

Chodziło mi o punkty P i Q.
Zakładasz, że one są środkami przeciwprostokątnych?

[octahedron]

Chodziło mi o punkty P i Q.
Zakładasz, że one są środkami przeciwprostokątnych?

Tak, pokazuję, że prosta poprowadzona przez te środki przechodzi też przez wierzchołki prostokąta, może nie dość jasno to napisałem.