Strona 1 z 1
Geometria analityczna
: 18 cze 2019, 15:54
autor: karolo48
1. Sprawdź, czy proste \(l_{1}=\frac{x-3}{1}=\frac{y-1}{-1}=\frac{z+1}{-2}\) oraz \(l_{2}=\frac{x+1}{-1}=\frac{y}{1}=\frac{z}{2}\) leżą na jednej płaszczyźnie. Jeśli tak, to wyznacz jej równanie. Sprawdź, czy podane proste są do siebie równoległe lub prostopadłe.
2. Napisz równanie parametryczne prostej l przechodzącej przez punkt P = (A, B, C) i prostopadłej do wektorów \(\overrightarrow{v_{1}}=[-1,2,3], \overrightarrow{v_{2}}=[5,1,0]\), gdzie A=\(i^{2016}\), B=\(Im[3i-2(1-i)^{2}+1]\), C=\(Re(\frac{2i}{1-i})\).
: 18 cze 2019, 22:08
autor: korki_fizyka
Sprytny zaw0dnik poszpera w internecie i pierwszy przybiegnie na metę bez dopingu
 http://matematyka.pisz.pl/forum/376373.html
https://matematyka.pl/238420.htm
http://matematyka.pisz.pl/forum/376373.html
https://matematyka.pl/238420.htm
: 20 cze 2019, 15:01
autor: panb
- 1. Zapisujemy równania prostych w postaci parametrycznej:
\(l_1: \begin{cases}x=t+3\\y=-t+1\\z=-2t-1 \end{cases},\quad l_2: \begin{cases}x=-y+1\\y=t\\z=2t \end{cases}\)
Równanie płaszczyzny zawierającej \(l_2\) (łatwiejszy zapis), to : \(A(-t+1)+Bt+2Ct+D=0 \iff (-A+B+2C)t+(A+D)=0\)
Ponieważ to ma być zerem dla każdego t, więc \(\begin{cases}-A+B+2C=0\\A+D=0 \end{cases} \So \begin{cases}A=A\\B=A-2C\\C=C\\D=-A \end{cases}\)
czyli płaszczyzna zawierająca prostą \(l_2\) ma równanie \(Ax+(A-2C)y+Cz-A=0\)
Czy można tak dobrać współczynniki, że by i prosta \(l_1\) leżała na tej płaszczyźnie?
Wstawiamy i otrzymujemy:
\(A(t+3)+(A-2C((-t+1)+C(-2t-1)-A=0 \iff 3A-3C=0 \iff C=A\).
Równanie płaszczyzny zawierającej obie proste istnieje i ma postać: \(Ax-Ay+Az-A=0\)
Przy \(A \neq 0\) daje to odpowiedź:
- Obie proste leżą na jednej płaszczyźnie o równaniu
\[x-y+z-1=0\]
Ponieważ iloczyn wektorowy \([1,-1,-2] \times [-1,1,2]=0\), więc uzyskujemy informację, że te proste są równoległe.
Co widać na załączonym obrazku!

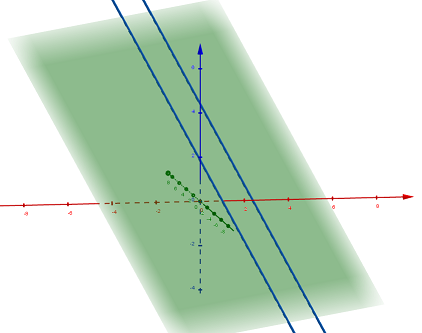
- rys2.png (54.97 KiB) Przejrzano 1199 razy