forum.zadania.info

Punkt A = (7, −1) jest wierzchołkiem trójkąta równoramiennego ABC, w którym AC = BC .
Obie współrzędne wierzchołka C są liczbami ujemnymi. Okrąg wpisany w trójkąt ABC ma
równanie \(x^2+y^2=10\). Oblicz współrzędne wierzchołków B i C tego trójkąta

Szkic rozwiązania wg mnie:
1. Wyznaczamy równania stycznych do okręgu i przechodzących przez punkt A
2. Na stycznej AC obieramy dowolny punkt C' np. x'=5 a y' wyliczamy z równania stycznej
3 Na stycznej AB obieramy punkt B(x,y) stycznej
4. Z warunku AC=BC wyliczamy współrzędne punktu B'
5. Trójkąt AB'C' jest podobny do trójkąta ABC, a prosta B'C' jest równoległa do szukanej prostej BC
6. Wspólczynnik kierunkowy prostej BC będziemy znali i wystarczy znaleźć wyraz wolny b (odległość prostej BC od środka okręgu)
7. Mając równanie prostej BC rozwiązujemy układ równań i wyznaczamy punkt C

Może ktoś ma inny pomysł na to zadanie

Wycofuję się z tego sposbu rozwiązania

Poprowadzenie stycznych do okręgu , przechodzących przez A załatwia problem ( dalej już łatwo).
Tylko , że ich poprowadzenie jest dość trudne rachunkowo ( nie mogę przez to przebrnąć ).

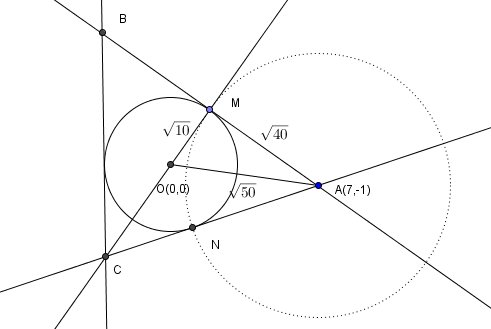
Dobra, wymyśliłam inaczej: wyznaczyć punkt M jako rozwiązanie układu równań
\(\begin{cases}x^2+y^2=10\\(x-7)^2+(y+1)^2=40 \end{cases}\)
Wychodzi \(M=(1,8;2,6)\)
Dalej chyba łatwo ale nie mam czasu sprawdzać.

No to dalej:
B=(x,y)
M jest środkiem odcinka AB czyli:\(\begin{cases} \frac{x+7}{2}=1,8\\ \frac{y-1}{2}=2,6 \end{cases}\)
stąd \(B=(-3,4;6,4)\)

Punkt N jest drugim rozwiązaniem układu \(\begin{cases}x^2+y^2=10\\(x-7)^2+(y+1)^2=40 \end{cases}\)
\(N=(1,-3)\)
Teraz należy znaleźć równania prostych OM oraz AN. Punkt C leży na ich przecięciu.

\(\vec{OM} =[1,8;2,6] \perp \left[ 26,-18\right] \parallel \left[ 13,-9\right]\)
prosta OM ma równanie:\(13x-9y=0\)

\(\vec{AN}= \left[ -6,-2\right] \parallel \left[-3,-1 \right] \perp \left[ 1,-3\right]\)
prosta AN ma równanie: \(x-3y+D=0\)
przy czym:\(1-3 \cdot (-3)+D=0\) czyli \(D=-10\)
no to prosta AN ma równanie: \(x-3y-10=0\)

Wspołrzędne punktu C wyznaczymy rozwiązując układ równań \(\begin{cases} 13x-9y=0\\x-3y-10=0\end{cases}\)
I otrzymamy \(C= \left(-3,- \frac{13}{3} \right)\)

Jeszcze raz:
Szukamy równań stycznych do okręgu \(x^2+y^2= \sqrt{10}\)i przechodzących przez punkt A(7,-1)
y=ax+b -1=7a+b b=-1-7a y=ax-1-7a ax-y-1-7a =0
\(\frac{|a*0-1*0-1-7a|}{ \sqrt{a^2+1} }= \sqrt{10}\ \ \\) \(a_1=- \frac{9}{13}\ \ a_2= \frac{1}{3}\)
Równania stycznych (odczytujemy z rysunku)
\(AB:\ \ y= -\frac{9}{13}x+ \frac{50}{13}\ \ \ \\)\(AC:\ \ y= \frac{1}{3}x- \frac{10}{3}\ \ \ \\)
Prosta prostopadła do prostej AB i przechodzącej przez punkt O(0,0)\(\ \ \ \ y= \frac{13}{9} x\)
Punkt C to punkt przecięcia prostych (układ równań):
C: \(\begin{cases} y= \frac{1}{3}x - \frac{10}{3} \\y= \frac{13}{9}x\end{cases}\)\(\ \ \ C=(-3;- \frac{13}{3})\)
Punkt D obliczamy z układu:
D: \(\begin{cases} y= -\frac{9}{13}x+ \frac{50}{13} \\y= \frac{13}{9} x\end{cases}\)\(\ \ \ D=( \frac{9}{5};\frac{13}{5})\)
Wyliczamy punkt \((x_B,y_B)\)
\(\frac{x_B+7}{2}=\frac{9}{5}\ \ \ x_B=- \frac{17}{5}\) \(\ \ \ \ \frac{y_B-1}{2}=\frac{13}{5}\ \ \ y_B= \frac{31}{5}\)
\(B=( -\frac{17}{5} ; \frac{13}{5})\)

Przepraszam mam kłopot z umieszczeniem rysunku