Strona 1 z 1
2 optymalizacyjne zadania ze stereometrii
: 19 mar 2018, 23:18
autor: Enio
1.
Rozpatrzmy graniastosłupy prawidłowe trójkątne, w których suma długości wszystkich krawędzi jest równa 9. a) Jaką największą objętość może mieć dany graniastosłup ?
b) Przez przekątną ściany bocznej graniastosłupa o największej objętości i środek przeciwległej krawędzi bocznej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju.
2.
Dany jest stożek, którego powierzchnia boczna jest wycinkiem koła o promieniu r i kącie środkowym 72(stopnie). Rozpatrzmy wszystkie graniastosłupy prawidłowe czworokątne wpisane w ten stożek : ich dolna podstawa zawiera się w podstawie stożka, a wierzchołki górnej należą do powierzchni bocznej stożka. Oblicz pole powierzchni bocznej tego graniastosłupa, którego objętość jest największa.
Re: 2 optymalizacyjne zadania ze stereometrii
: 20 mar 2018, 12:13
autor: radagast
Enio pisze:1.
Rozpatrzmy graniastosłupy prawidłowe trójkątne, w których suma długości wszystkich krawędzi jest równa 9. a) Jaką największą objętość może mieć dany graniastosłup ?
b) Przez przekątną ściany bocznej graniastosłupa o największej objętości i środek przeciwległej krawędzi bocznej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju.
a)
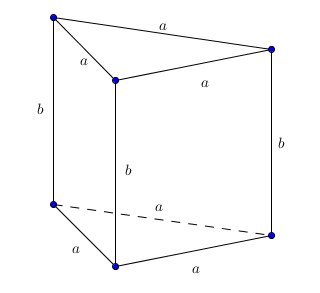
- ScreenHunter_266.jpg (7.28 KiB) Przejrzano 2274 razy
\(a \in \left(0, \frac{3}{2} \right),b \in \left( 0,3\right)\)
\(V(a,b)= \frac{a^2 \sqrt{3} }{4}b\)
\(6a+3b=9 \So b=3-2a\)
\(V(a)= \frac{a^2 \sqrt{3} }{4} \left( 3-2a\right)= -\frac{ \sqrt{3} }{2}a^3 +\frac{ 3\sqrt{3} }{4}a^2\)
No i należy znaleźć największą wartość tej funkcji w przedziale
\(\left(0, \frac{3}{2} \right)\)
Napisz co Ci wyszło , to pomogę zrobić b)
Re: 2 optymalizacyjne zadania ze stereometrii
: 20 mar 2018, 14:08
autor: radagast
Enio pisze:
2.
Dany jest stożek, którego powierzchnia boczna jest wycinkiem koła o promieniu r i kącie środkowym 72(stopnie). Rozpatrzmy wszystkie graniastosłupy prawidłowe czworokątne wpisane w ten stożek : ich dolna podstawa zawiera się w podstawie stożka, a wierzchołki górnej należą do powierzchni bocznej stożka. Oblicz pole powierzchni bocznej tego graniastosłupa, którego objętość jest największa.
Nieco trudniejsze od 1.
\(R\) -promień podstawy stożka
\(r\) -tworząca stożka
\(H\) -wysokość stożka
Zacznijmy od tego,że pole powierzchni bocznej to wycinek koła. Czyli
\(\frac{72}{360}= \frac{\pi Rr}{\pi r^2}\)
stąd
\(R= \frac{1}{5} r\)
\(H= \sqrt{(5R)^2-R^2} =2R \sqrt{6}\)
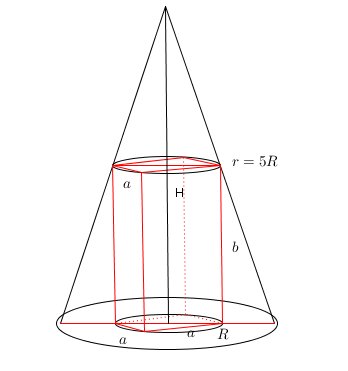
- ScreenHunter_268.jpg (12.1 KiB) Przejrzano 2270 razy
\(a,b\)-krawędzie graniastosłupa.
\(a \in \left(0,R \right)\) czyli
\(a \in \left(0, \frac{1}{5}r \right)\)
Z twierdzenia Talesa mamy:
\(\frac{a \sqrt{2} }{2R}= \frac{H-b}{H}\)
czyli, o ile się nie pomyliłam w rachunkach ( co jest wątpliwe, zwykle się mylę)
\(b= \frac{2 r \sqrt{6}-5a \sqrt{12}}{5}\)
No i teraz jak zwykle:
\(V(a,b)=...\)
\(V(a)=...\)
I znaleźć największą wartość funkcji
\(V(a)\) w odpowiednim przedziale.
PS to co powyżej należy traktować jak szkic rozwiązanie. Wymaga szczegółowego sprawdzenia.
Re: 2 optymalizacyjne zadania ze stereometrii
: 20 mar 2018, 21:03
autor: Enio
radagast pisze:Enio pisze:1.
Rozpatrzmy graniastosłupy prawidłowe trójkątne, w których suma długości wszystkich krawędzi jest równa 9. a) Jaką największą objętość może mieć dany graniastosłup ?
b) Przez przekątną ściany bocznej graniastosłupa o największej objętości i środek przeciwległej krawędzi bocznej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju.
a)
ScreenHunter_266.jpg
\(a \in \left(0, \frac{3}{2} \right),b \in \left( 0,3\right)\)
\(V(a,b)= \frac{a^2 \sqrt{3} }{4}b\)
\(6a+3b=9 \So b=3-2a\)
\(V(a)= \frac{a^2 \sqrt{3} }{4} \left( 3-2a\right)= -\frac{ \sqrt{3} }{2}a^3 +\frac{ 3\sqrt{3} }{4}a^2\)
No i należy znaleźć największą wartość tej funkcji w przedziale
\(\left(0, \frac{3}{2} \right)\)
Napisz co Ci wyszło , to pomogę zrobić b)
Wyszło mi a = 1
Mógłabyś z b pomóc ?
: 20 mar 2018, 21:22
autor: radagast
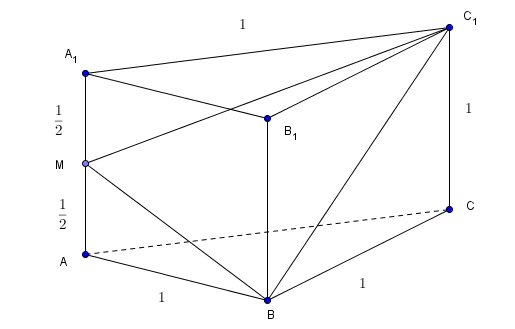
- ScreenHunter_269.jpg (15.93 KiB) Przejrzano 2266 razy
No to mamy do policzenia pole trójkąta
\(BC_1M\). Policz jego boki i powiedz co Ci wyszło
