Strona 1 z 1
Nierówność logarytmiczna
: 08 lis 2017, 17:06
autor: poetaopole
Wykaż, że \(log _{4}5+log _{5}4>log _{5}6 +log _{6}5\).
: 09 lis 2017, 10:54
autor: korki_fizyka
Zastosuj wzory: na zamianę podstaw log oraz na sumę a potem pozostanie do rozwiązania prosta, pojedyńcza nierówność.
: 09 lis 2017, 11:01
autor: radagast
Czy mówisz o takiej nierówności :
\(\log_54 \cdot \log_56<1\) ?
Ona nie jest prosta !
Męczę się z tą nierównością od wczoraj i stoję w miejscu. Może mam zaćmienie ? Nie idzie. Wiem , że jest prawdziwa (sprawdziłam przy pomocy komputera). Prawa strona większa , choć niewiele.
- ScreenHunter_1943.jpg (15.95 KiB) Przejrzano 2187 razy
: 09 lis 2017, 11:47
autor: radagast
A jakby tak pokazać, że dla każdego
\(x>1\) zachodzi nierówność
\(\ln(x-1)\ln(x+1)<\ln^2x\)
to by wystarczyło ale też nie umiem tego pokazać (chociaż to jest prawda):
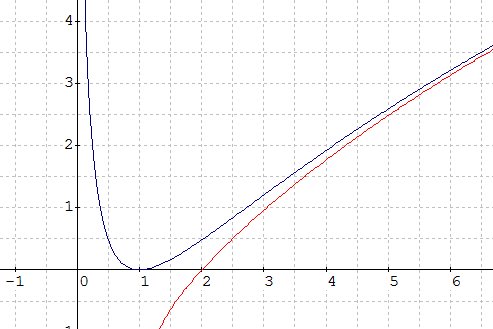
- ScreenHunter_1944.jpg (30.78 KiB) Przejrzano 2179 razy
: 09 lis 2017, 12:53
autor: korki_fizyka
Przepraszam nie zrozumiałem polecenia inaczej bym swoich 3 groszy nie wtrącił, bo omijam wszelkie wykaż,że

Jako fizyk jestem bardziej praktyczny i dla mnie widać to po prostu gołym okiem (czytaj z definicji logarytmu), że jeżeli przegrupujemy nierówność:
\(log _{5}4-log _{5}6>log _{6}5-log _{4}5\)
teraz stosując to co zalecałem wcześniej mamy:
\(log _{5} \frac{2}{3}> \frac{log _{5} \frac{2}{3}}{log _{5}6log _{5}4}\)
mianownik ułamka po prawej stronie jest < 1 i
\(log _{5} \frac{2}{3}\) też jest mniejsze od jedynki więc...cbdo
tutaj jest coś nt.
https://www.zadania.info/d1432/6904961
Re:
: 09 lis 2017, 13:06
autor: radagast
korki_fizyka pisze:
mianownik ułamka po prawej stronie jest < 1
A mógłbyś to udowodnić ? (Rzecz jest moim zdaniem niebanalna)
: 09 lis 2017, 13:15
autor: poetaopole
Już mam, napisze wieczorem. Rozwiązanie jest prześliczne... Sam na nie jednak nie wpadłem... pomógł mi... WROCŁAW.
: 09 lis 2017, 13:20
autor: poetaopole
Wystarczy sprytnie użyć
\(( \frac{a+b}{2})^2 \ge ab\) do oszacowania. Wieczorem napiszę gdzie i jak. Teraz muszę się uczyć

: 09 lis 2017, 14:08
autor: poetaopole
Pokazujemy, że \(\log_{5}4 \cdot \log_{5}6<1\).
Korzystamy ze znanej formuły: \(( \frac{a+b}{2})^2 \ge ab\) do oszacowania powyższej nierówności.
\(\log_{5}4 \cdot \log_{5}6 \le \left( \frac{\log_{5}4 + \log_{5}6}{2} \right)^2< \left( \frac{\log_{5}25}{2} \right)^2=1\).
Prawda, że PIĘKNE? Piękne w swojej PROSTOCIE...
Re: Nierówność logarytmiczna
: 09 lis 2017, 15:01
autor: radagast
Tak , to rzeczywiście jest ładne i można to zastosować do "mojego" uogólnienia i pokazać (tą samą metodą),że
\(\ln(x-1)\ln(x+1)<\ln^2x\):
\(\ln(x-1)\ln(x+1)\le \left(\frac{\ln(x-1)+\ln(x+1)}{2} \right) ^2= \left(\frac{\ln(x^2-1)}{2} \right) ^2< \left(\frac{\ln(x^2)}{2} \right) ^2=\ln^2x\) (oczywiście dla x>1, bo tylko wtedy to ma sens)
: 09 lis 2017, 15:11
autor: poetaopole
No to mamy ładne zadanie z logarytmami naturalnymi dla studentów I roku ze WSTĘPU DO MATEMATYKI. Zastanawiam się, czy nie można by TEGO użyć gdzieś w szeregach albo całkach niewłaściwych? Może ktoś się pokusi o wymyślenie zadania z wykorzystaniem nierówności Pani RADAGAST? Nierówność jest ŚLICZNA

Myślę, że własnie odkryliśmy (ja mam w tym minimalny udział) nierówność, która być może przejdzie do historii matematyki?