Strona 1 z 1
Równanie trygonometryczne
: 03 lut 2017, 15:36
autor: Asiaseek
Rozwiązać równanie \(sin \frac{x}{2} + cos \frac{x}{2} = \sqrt{2} sin x\)
: 03 lut 2017, 16:15
autor: Galen
Podnosisz obustronnie do kwadratu.
\(sin^2(\frac{x}{2})+cos^2(\frac{x}{2})+2sin( \frac{x}{2} )cos( \frac{x}{2} )=2sin^2x\)
\(1+sinx=2sin^2x\\2sin^2x-sinx-1=0\\\Delta=1+8=9=3^2\\sinx= \frac{1-3}{4}=- \frac{1}{2}\;\;lub\;\;sinx=1\)
\(x=- \frac{\pi}{6}+2k\pi\\lub\\x= \frac{7}{6}\pi+2k\pi\\lub\\x= \frac{\pi}{2}+2k\pi\;\;\;i\;\;\;k\in C\)
Podnoszenie do kwadratu może doprowadzić do "pierwiastków obcych" ,więc trzeba sprawdzać ,które liczby spełniają równanie.
\(x= \frac{\pi}{2}\\sin45^o+cos45^o= \frac{ \sqrt{2} }{2}+ \frac{ \sqrt{2} }{2}= \sqrt{2}=lewa\;str.\\P= \sqrt{2} \cdot sin90^o= \sqrt{2}\\L=P\)
Sprawdzenie pozostałych jest bardziej pracochłonne,ale wierzę w Twoją pracowitość

: 03 lut 2017, 16:24
autor: panb
Podnoszenie do kwadratu bywa zdradliwe (też tak zrobiłem, ale mnie uczono, żeby wtedy sprawdzić rozwiązanie).
Oto co się okazało:
- Weźmy \(x= \frac{\pi}{2} +2\pi= \frac{5}{2}\pi \\
L=\sin \frac{5}{4}\pi+\cos \frac{5}{4}\pi=-\sqrt2 ,\quad P=\sqrt2\sin \frac{5}{2}\pi=\sqrt2 \So P\neq L\).
Liczba \(x= \frac{\pi}{2} +2\pi\) NIE JEST rozwiązaniem równania.
Re: Równanie trygonometryczne
: 03 lut 2017, 16:56
autor: radagast
Asiaseek pisze:Rozwiązać równanie \(sin \frac{x}{2} + cos \frac{x}{2} = \sqrt{2} sin x\)
\(\sin \frac{x}{2} + \cos \frac{x}{2} = \sqrt{2} \sin x\)
\(\sin \frac{x}{2} + \sin \left(\frac{ \pi }{2} -\frac{x}{2} \right) = \sqrt{2} \sin x\)
\(2\sin \frac{\pi}{4}\cos \frac{x-\frac{ \pi }{2} }{2} = \sqrt{2} \sin x\)
\(\cos \frac{x-\frac{ \pi }{2} }{2} = \sin x\)
\(\cos \left( \frac{x}{2}- \frac{\pi}{4} \right) = \cos \left( x-\frac{\pi}{2} \right)\)
\(\frac{x}{2}- \frac{\pi}{4} = x-\frac{\pi}{2}+2k\pi\ \ \ \vee \ \ \ \frac{x}{2}- \frac{\pi}{4} = \frac{\pi}{2}-x+2k\pi\)
\(\frac{x}{2}-x = \frac{\pi}{4} -\frac{\pi}{2}+2k\pi\ \ \ \vee \ \ \ x+\frac{x}{2} = \frac{\pi}{4} + \frac{\pi}{2}+2k\pi\)
\(-\frac{x}{2} = - \frac{\pi}{4} +2k\pi\ \ \ \vee \ \ \ \frac{3x}{2} = \frac{3\pi}{4} + 2k\pi\)
\(\frac{x}{2} = \frac{\pi}{4} +2k\pi\ \ \ \vee \ \ \ \frac{3x}{2} = \frac{3\pi}{4} + 2k\pi\ \ \ \ k \in C\)
\(x = \frac{\pi}{2} +4k\pi\ \ \ \vee \ \ \ 3x= \frac{3\pi}{2} + 4k\pi\ \ \ \ k \in C\)
\(x = \frac{\pi}{2} +4k\pi\ \ \ \vee \ \ \ x= \frac{\pi}{2} + k \frac{4 \pi }{3} \ \ \ \ k \in C\)
\(x= \frac{\pi}{2} + k \frac{4 \pi }{3} \ \ \ \ k \in C\) (ten pierwszy ciąg zawiera się w tym drugim)
: 03 lut 2017, 17:55
autor: radagast
A wygląda to tak :
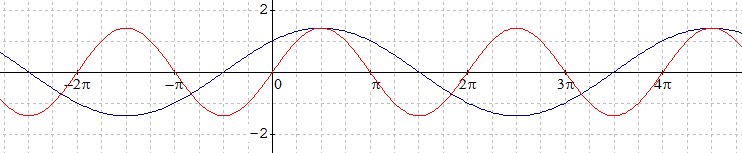
- ScreenHunter_1777.jpg (29.98 KiB) Przejrzano 1670 razy