forum.zadania.info

Wysokość trójkątnego ostrosłupa prawidłowego ma długość h, a krawędzie boczne
są do siebie prostopadłe. Wyznacz długość promienia i pole powierzchni kuli
opisanej na tym ostrosłupie.

Szkoda, że nie podałeś odpowiedzi, bo nie jestem pewna, czy dobrze myślę.
Wysokość ostrosłupa tworzy z krawędzią boczną i promieniem okręgu opisanego na trójkącie podstawy trójkąt prostokątny.
Jeżeli oznaczymy: a- krawędź podstawy, b- krawędź boczna, to ponieważ ściana boczna jest trójkątem prostokątnym równoramiennym, więc \(a=b\sqrt{2}\). Promień okręgu opisanego na trójkącie podstawy ma długość \(\frac{a\sqrt{3}}{3}\), czyli \(R=\frac{b\sqrt{6}}{3}\).
Z twierdzenia Pitagorasa:
\(h^2+(\frac{b\sqrt{6}}{3})^2=b^2\\h^2=\frac{1}{3}b^2\\b^2=3h\\b=h\sqrt{3}\\R=h\sqrt{2}\)

Jeśli połączymy środek kuli z wierzchołkiem ostrosłupa, w którym zbiegają się krawędzie boczne ostrosłupa oraz z wierzchołkiem podstawy ostrosłupa, to otrzymamy trójkąt równoramienny, w którym ramionami są promienie kuli (r), podstawą jest krawędź boczna. wysokość tego trójkąta poprowadzone na ramię to promień R. Wysokość ta dzieli ramię na odcinki o długości h - r-h.
Z twierdzenia Pitagorasa:
\((r-h)^2+R^2=r^2\\r^2-2rh+h^2+(h\sqrt{2})^2=r^2\\3h^2-2rh=0\\3h=2r\\r=\frac{3}{2}h\)

Pole powierzchni kuli:
\(P_k=4\pi\cdot\ r^2\\P_k=4\pi\cdot\frac{9}{4}h^2\\P_k=9\pi\ h^2\)

W tym rozwiązaniu założyłam (bo to wynikło z obserwacji zależności między danymi), że promień kuli jest większy od wysokości ostrosłupa. Ale gdyby wysokość tego ostrosłupa była większa od promienia kuli, wtedy trójkąt równoramienny, opisany w rozwiązaniu byłby rozwartokątny, wysokość spadałaby poza trójkątem i twierdzenie Pitagorasa:
\((h-r)^2+R^2=r^2\), co daje dokładnie to samo rozwiązanie.

a moge prosic o rysunek? łatwiej byłoby mi sobie to wyobrazić

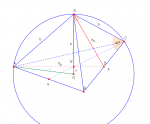
Robiłam trochę inaczej, ale wyszło to samo co Irenie, więc chyba jest dobrze.

Trójkąt \(BCS\) jest prostokątny i równoramienny.
\(|<DCS|=45^o\)
więc \(|SD|=|DC|= \frac{1}{2}a\)

Podstawą ostrosłupa jest trójkąt równoboczny, więc
\(h_p= \frac{a \sqrt{3} }{2}\)
\(|AS'|= \frac{2}{3}h_p= \frac{2}{3} \cdot \frac{a \sqrt{3} }{2}=\frac{a \sqrt{3} }{3}\)
\(|S'D|= \frac{1}{3}h_p= \frac{1}{3} \cdot \frac{a \sqrt{3} }{2}=\frac{a \sqrt{3} }{6}\)

Z twierdzenia Pitagorasa dla trójkąta \(S'DS\)
\(|SD|^2=|S'S|^2+|S'D|^2\)
\(( \frac{1}{2}a )^2=h^2+(\frac{a \sqrt{3} }{6})^2\)
\(a=h \sqrt{6}\)

Z twierdzenia Pitagorasa dla trójkąta \(AS'O\)
\(|AS'|^2+|S'O|^2=|AO|^2\)
\(|S'O|=x=r-h\)
\((\frac{a \sqrt{3} }{3})^2+(r-h)^2=r^2\)
\((\frac{h \sqrt{6} \cdot \sqrt{3} }{3})^2+(r-h)^2=r^2\)
\(2h^2+h^2 - 2hr + r^2=r^2\)
\(r= \frac{3}{2} h\)