Strona 4 z 5
: 23 gru 2012, 15:30
autor: kejkun
Re: Konkurs KUL
: 23 gru 2012, 15:35
autor: denatlu
to żadna sinusoida nie jest. Wykres
\(f(x)\) idzie tak:
\(\wedge\) dla każdej jednostki, czyli nad
\(x=0\) i
\(x=1\) jest namiot(
\(\wedge\)), między
\(x=1\) i
\(x=2\) i tak dalej.
PS: czekam na dalsze odpowiedzi

Re: Konkurs KUL
: 23 gru 2012, 15:37
autor: kamil13151
denatlu pisze:to żadna sinusoida nie jest.
Oczywiście, że nie jest. Chyba cudzysłów to nie był dobry pomysł

Kejkun wyobraź sobie prostą i wykres tej funkcji na odcinku 0-2.
: 23 gru 2012, 15:38
autor: kejkun
skąd pomysł, że jest to namiot ?
sądzę, że hm
wyobraziłeś to sobie dla zbyt mało argumentów po-śrendnich

wtedy z namiotu robi się sinusoida

>?
nie czaje czemu liczycie to podwójnie ;o.
jak prosta przebija to w 1 punkcie bodajże ;x
ten nawet namiot ^
nasz ;x
a dalej dla innego argumentu w 2 miejscu.
: 23 gru 2012, 15:41
autor: kamil13151
Re:
: 23 gru 2012, 15:43
autor: denatlu
denatlu pisze:Dla \(x=2\) odległość do punktu(x) o współrzędnej całkowitej jest równa \(0\), bo \(x=2\) jest całkowite. Dla \(x=2\frac{1}{2}\) odległość do najbliższego punktu o współrzędnej całkowitej jest \(\frac{1}{2}\). Czyli \(f(2)=0\) a \(f(2\frac{1}{2})=\frac{1}{2}\). Dla \(x=1.3\) odległość wynosi \(0.3\) czyli \(f(1.3)=0.3\). I to jest wykres funkcji \(f(x)\).
\(f(2)=0 \\
f(2.3)=0.3 \\
f(2\frac{1}{2})=\frac{1}{2} \\
f(2.6)=0.4 \\
f(3)=0\)
Narysuj to i w nagrodę podaj mi jakieś odpowiedzi do innych zadań

. Musze lecieć teraz. Cześć!
: 23 gru 2012, 15:43
autor: kejkun
no, ale czemu liczycie podwójnie
. jak ja widzę dla jakiegos tam argumentu 1 przeciecie,
dla nastepnego drugie ???
itd ..
hm ?
Re:
: 23 gru 2012, 16:07
autor: radagast
kejkun pisze:nie czaję tego zadania 22.
jakby ktoś mógł wyjaśnić
.
np. " .. od najbliższego punktu o współrzędnej całkowitej "
no tak, ale której współrzędnej " x " czy " y " ??
funkcja
\(f\) to zwykła część ułamkowa (t.zw. mantysa).
Rysowanie jej wykresu jest dobrym pomysłem. widać wtedy, że podane równanie ma 2012 rozwiązań.
Choć , prawdę mówiąc, moim zdaniem , to ich będzie 2011, ale nie ma takiej odpowiedzi

: 23 gru 2012, 17:23
autor: radagast
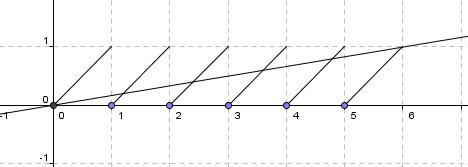
- ScreenHunter_1226.jpg (11.46 KiB) Przejrzano 2508 razy
Narysowałam tę sytuację dla 6:
i wtedy jest 5 rozwiązań.
No moim zdaniem , dla 2012 będzie ich 2011. Dlaczego nie ma takiej odpowiedzi ?

: 23 gru 2012, 17:42
autor: radagast
aaa już wiem!, to nie będzie mantysa ale podobnie.
dla 6 sytuacja wygląda tak:
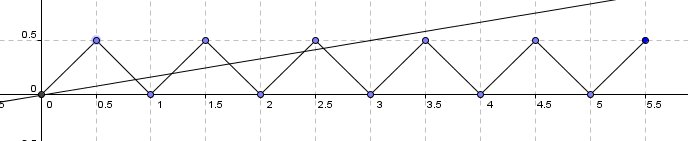
- ScreenHunter_1228.jpg (16.24 KiB) Przejrzano 2504 razy
6 rozwiązań. Dla 2012 będzie ich 2012. Odpowiedź D
: 25 gru 2012, 23:44
autor: patryk00714
12 odpowiedź c)
: 25 gru 2012, 23:55
autor: octahedron
\(12.\,\sin\alpha+\sqrt{3}\cos\alpha=2\cdot\(\frac{1}{2}\sin\alpha+\frac{\sqrt{3}}{2}\cos\alpha\)=2\cdot\(\cos\frac{\pi}{3}\sin\alpha+\sin\frac{\pi}{3}\cos\alpha\)=2\sin\(\alpha+\frac{\pi}{3}\)\in[-2,2]\)
Re: Konkurs KUL
: 25 gru 2012, 23:56
autor: patryk00714
14.
Oczywiście mowa tu o zbiorach więc pisząc A, mam na myśli \(\overline{\overline{A}}\)
\(A =12\)- angielski
\(H=10\)- hiszpański
\(R=11\) - rosyjski
\(H \cap R=7\) - rosyjski i hiszpański
\(A \cap H =5\) - rosyjski i hiszpański
\(R \cap A =6\) - rosyjski i angielski
\(A \cap H \cap R=3\) - wszystkie
Policzymy ilu tłumaczy znało przynajmniej jeden z tych języków, czyli szukamy \(A \cup H \cup R\)
mamy: \(A \cup H \cup R=A+B+C-A\cap R -A\cap H -H\cap R +A\cap R \cap H=12+10+11-7-5-6+3=18\)
czyli żadnego z tych języków nie znały \(20-18=2\) osoby
odp C
: 26 gru 2012, 00:11
autor: octahedron
15. Jeśli jedną oś symetrii odbijemy względem drugiej osi, to otrzymana prosta też jest osią symetrii. Tutaj są tylko dwie, więc muszą być prostopadłe, wtedy każda sama jest swoim odbiciem względem drugiej, a ich punkt przecięcia jest środkiem symetrii.
odp. A,C,D
Re: Konkurs KUL
: 26 gru 2012, 00:12
autor: patryk00714
16. Rozumiem, że chodzi tylko o pierwiastki rzeczywiste.
\(x^4-10x^2+9=a \;\;\;\ a \in \R\)
czyli \(x^4-10x^2+9-a=0\)
\(t=x^2 \;\;\;\ t \ge 0\)
\(t^2-10t+9-a=0\)
\(\Delta=100-36+4a=64+4a\)
Jeżeli delta będzie większa od zera to równanie \(x^4-10x^2+9=a \;\;\;\ a \in \R\), może mieć albo 2 pierwiastki (gdy \(t_1>0 \;\;\ t_2<0 \;\;\;\;\ np. a=20\)), albo 4 pierwiastki (gdy \(t_1,t_2>0\;\;\;\;\ np. \;\;\ a=0\)), albo 3 pierwiastki (gdy \(t_1=0, t_2>0 \;\;\;\;\ np. \;\;\ a=9\)), jeden będzie miało gdy \(t_1=0 \;\;\ t_2<0\), ale takiej sytuacji nie otrzymamy nigdy, bo \(-b=10 \;\;\ wspolczynnik\;\ kierunkowy: \;\;\ a=1>0\), a z tego wynika, że aby jeden był zerem to musimy odjąc pierwiastek z delty, zatem do drugiego ten pierwiastek trzeba dodać i wtedy mamy wszystkie wyrazy dodatnie, a więc wtedy otrzymamy drugie pierwiastek dodatni, co nam psuje ten przypadek.
Zatem B,C,D