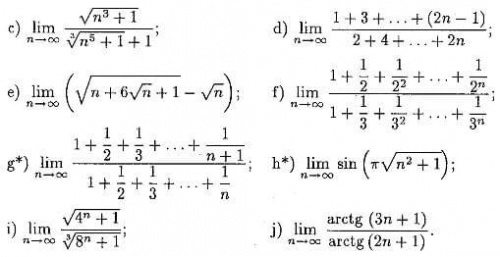Granice, pochodne, całki, szeregi
Otrzymałeś(aś) rozwiązanie do zamieszczonego zadania? - podziękuj autorowi rozwiązania! Kliknij
celia11
Fachowiec
Posty: 1860 Rejestracja: 22 lut 2009, 15:26Podziękowania: 341 razy Otrzymane podziękowania: 5 razy
Post
autor: celia11 24 lut 2011, 19:58
proszę o pomoc w rozwiązaniu:
Korzystajac z twierdzenia o arytmetyce granic obliczyć podane granice ciagów:
dziękuję
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 24 lut 2011, 20:36
c) \(\lim_{n\to \infty } \frac{ \sqrt{n^3+1}}{ \sqrt[3]{n^5+1}+1 }=\) \(\lim_{n\to \infty } \frac{ \sqrt{1+ \frac{1}{n^3} }}{ \sqrt[6]{ \frac{n^{10}+2n^5+1}{n^9} }+ \frac{1}{ \sqrt{n^3} } }= \frac{1}{ \infty }=0\)
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 24 lut 2011, 20:43
d)\(\lim_{n\to \infty } \frac{1+3+...+(2n-1)}{2+4+...+2n}=\) \(\lim_{n\to \infty } \frac{\frac{1+(2n-1)}{2}n}{\frac{2+2n}{2}n} =\) \(\lim_{n\to \infty } \frac{2n}{2+2n} =\) \(\lim_{n\to \infty } \frac{n}{1+n} =\) \(\lim_{n\to \infty } \frac{1}{ \frac{1}{n} +1} = 1\)
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 24 lut 2011, 20:52
e)\(\lim_{n\to \infty } ( \sqrt{n+6 \sqrt{n}+1 } - \sqrt{n} )=\) \(\lim_{n\to \infty } \frac{ n+6 \sqrt{n}+1 - n }{ \sqrt{n+6 \sqrt{n}+1 } + \sqrt{n} } =\) \(\lim_{n\to \infty } \frac{6 + \frac{1}{\sqrt{n}} }{ \sqrt{1+ \frac{6}{\sqrt{n}} + \frac{1}{n} } + 1 } =3\)
celia11
Fachowiec
Posty: 1860 Rejestracja: 22 lut 2009, 15:26Podziękowania: 341 razy Otrzymane podziękowania: 5 razy
Post
autor: celia11 24 lut 2011, 20:57
radagast pisze: e)\(\lim_{n\to \infty } ( \sqrt{n+6 \sqrt{n}+1 } - \sqrt{n} )=\) \(\lim_{n\to \infty } \frac{ n+6 \sqrt{n}+1 - n }{ \sqrt{n+6 \sqrt{n}+1 } + \sqrt{n} } =\) \(\lim_{n\to \infty } \frac{6 + \frac{1}{\sqrt{n}} }{ \sqrt{1+ \frac{6}{\sqrt{n}} + \frac{1}{n^2} } + \frac{1}{n} } =6\)
nie wiem czy w odpowiedziach jest źle: tam jest 3.
??
bardzo dziękuję
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 24 lut 2011, 21:02
U mnie był błąd, juz poprawiłam (nawet dwa, ale jeden nie miał wpływu na wynik)
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 24 lut 2011, 21:02
Podaj pozostałe odpowiedzi.
celia11
Fachowiec
Posty: 1860 Rejestracja: 22 lut 2009, 15:26Podziękowania: 341 razy Otrzymane podziękowania: 5 razy
Post
autor: celia11 24 lut 2011, 21:06
f) \(\frac{4}{3}\) \(1\) \(0\) \(1\) \(1\)
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 24 lut 2011, 21:16
f)\(\lim_{n\to \infty } \frac{1+ \frac{1}{2}+ \left( \frac{1}{2} \right)^2+...+ \left( \frac{1}{2} \right)^n }{1+ \frac{1}{3}+ \left( \frac{1}{3} \right)^2+...+ \left( \frac{1}{3} \right)^n }=\) \(\lim_{n\to \infty } \frac{ \frac{1- \left( \frac{1}{2} \right)^n } { 1- \frac{1}{2} }}{ \frac{1- \left( \frac{1}{3} \right)^n } { 1- \frac{1}{3} }} = \frac{ \frac{1 } { 1- \frac{1}{2} }}{ \frac{1 } { 1- \frac{1}{3} }}= \frac{}{} 2 \cdot \frac{2}{3} = \frac{4}{3}\)
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 24 lut 2011, 21:27
g)\(1+ \frac{1}{2} + \frac{1}{3} +...+ \frac{1}{n}+...= \infty\) bo to szereg harmoniczny\(1+ \frac{1}{2} + \frac{1}{3} +...+ \frac{1}{n} = S_n\) \(\lim_{n\to \infty } \frac{1+ \frac{1}{2} + \frac{1}{3} +...+ \frac{1}{n+1}}{1+ \frac{1}{2} + \frac{1}{3} +...+ \frac{1}{n}}=\(\lim_{n\to \infty } \frac{ S_n+ \frac{1}{n+1}}{S_n}=\) \(\lim_{n\to \infty } \frac{ 1+ \frac{1}{(n+1)S_n}}{1}=1\) \)
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 24 lut 2011, 21:32
h)
Nie wiem po co ta gwiazdka, ono jest najłatwiejsze . To jest ciąg stale równy 0 (sin całkowitych wielokrotności
\(\pi\) ), to pewnie tak dla zmylenia przeciwnika
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 24 lut 2011, 21:56
i) \(\lim_{n \to\infty } \frac{ \sqrt{4^n+1} }{ \sqrt[3]{8^n+1} }\) \(\lim_{n \to \infty } \frac{ \sqrt[6]{(4^n+1)^3} }{ \sqrt[6]{(8^n+1)^2} }\) \(\lim_{n \to \infty } \frac{ \sqrt[6]{(2^{2n}+1)^3} }{ \sqrt[6]{(2^{3n}+1)^2} }\) \(\lim_{n \to \infty } \frac{ \sqrt[6]{2^{6n} +3 \cdot 2^{4n} +3\cdot2^{2n}+ 1} }{ \sqrt[6]{2^{6n}+2 \cdot 2^{3n} +1} }\) \(\lim_{n \to \infty } \frac{ \sqrt[6]{1 + \frac{3}{2^{2n}} +\frac{3}{2^{4n}} + \frac{1}{2^{6n} } } }{ \sqrt[6]{1+\frac{2}{2^{3n}} +\frac{1}{2^{6n}} }}=1\)
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 24 lut 2011, 22:03
j)\(\lim_{n\to \infty } \frac{arctg(3n+1) }{arctg(2n+1)}= \frac{ \frac{ \pi }{2} }{\frac{ \pi }{2} } =1\)
celia11
Fachowiec
Posty: 1860 Rejestracja: 22 lut 2009, 15:26Podziękowania: 341 razy Otrzymane podziękowania: 5 razy
Post
autor: celia11 25 lut 2011, 11:14
radagast pisze: c) \(\lim_{n\to \infty } \frac{ \sqrt{n^3+1}}{ \sqrt[3]{n^5+1}+1 }=\) \(\lim_{n\to \infty } \frac{ \sqrt{1+ \frac{1}{n^3} }}{ \sqrt[6]{ \frac{n^{10}+2n^5+1}{n^9} }+ \frac{1}{ \sqrt{n^3} } }= \frac{1}{ \infty }=0\)
prosze mi pomóc w zrozumieniu, dlaczego jest tak rozwiazane, przez co były dzielone konkretne liczby, albo co było wyłączone przez pierwiastek.
dziekuję
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 25 lut 2011, 11:41
nie, jest ok . Tylko wytłumaczyłam się z tego działa nia dobrze , bo ja licznik i mianownik dzielę przez \(\sqrt{n^3}\) . Wczoraj sięz tym okropnie gimnastykowałam. Ale jest ok.