Mam projekt obróbki drewna, nad którym pracuję, i nie znam wzoru na obliczenie pomiaru. Każda pomoc w tej sprawie byłaby mile widziana.
Mając okrąg o promieniu r i cięciwę o długości x, jaki jest wzór na obliczenie wysokości y odcinka wyznaczonego przez cięciwę?
Znalazłem wzór na pole segmentu, ale nie mam wzoru na wysokość. Minęło 30 lat, odkąd wziąłem trygonometrię na studiach, więc każda pomoc, której możesz udzielić, byłaby bardzo mile widziana. TIA.
Problem z obróbką drewna
Otrzymałeś(aś) rozwiązanie do zamieszczonego zadania? - podziękuj autorowi rozwiązania! Kliknij
-
Tulio
- Stały bywalec

- Posty: 336
- Rejestracja: 29 paź 2010, 12:44
- Podziękowania: 21 razy
- Otrzymane podziękowania: 92 razy
- Płeć:
Re: Problem z obróbką drewna
Jak dobrze rozumiem mamy tę sytuację:
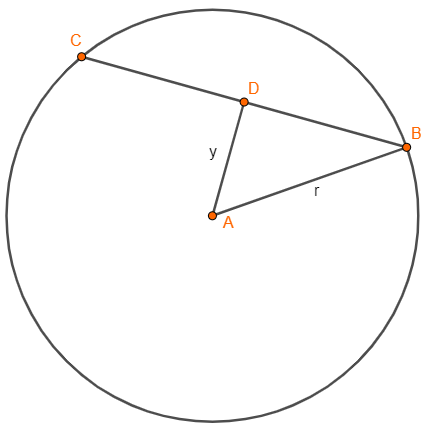
Zatem oznaczmy \(|BC|=x, |BD|=|DC|= \frac{x}{2} \). Wtedy:
\( \left( \frac{x}{2} \right) ^2 + y^2 = r^2\)
\( y^2 = r^2 - \frac{x^2}{4}\)
więc Twój wzór to:
\( y = \sqrt{r^2 - \frac{x^2}{4}} \)
co można zapisać też tak:
\( y = \frac{1}{2} \sqrt{4r^2-x^2} \)

Zatem oznaczmy \(|BC|=x, |BD|=|DC|= \frac{x}{2} \). Wtedy:
\( \left( \frac{x}{2} \right) ^2 + y^2 = r^2\)
\( y^2 = r^2 - \frac{x^2}{4}\)
więc Twój wzór to:
\( y = \sqrt{r^2 - \frac{x^2}{4}} \)
co można zapisać też tak:
\( y = \frac{1}{2} \sqrt{4r^2-x^2} \)
-
maria19
- Stały bywalec

- Posty: 425
- Rejestracja: 31 maja 2019, 19:32
- Podziękowania: 347 razy
- Otrzymane podziękowania: 98 razy
Re: Problem z obróbką drewna
Gotowe tabele wysokości opuszczonej na cieciwę znajdziesz w Poradniku encyklopedycznym matematyna I.N. Bronsztejna, do wyguglania.