Witam szanownych forumowiczów. Mam problem z pewnym zadaniem.
Treść:
Wyznaczyć przebieg zmienności funkcji i narysować wykres \(y=1+xe^{2/x}\)
Gdyby znalazła się osoba chętna poświęcić swój cenny czas byłbym bardzo wdzięczny.
Przebieg zmienności funkcji
Otrzymałeś(aś) rozwiązanie do zamieszczonego zadania? - podziękuj autorowi rozwiązania! Kliknij
No cóż dosyć standardowe. To po kolei:
Dziedzina \(D_f=\mathbb{R}\setminus\{0\}\)
Granice na krańcach dziedziny (będą cztery)
\(\lim\limits_{x\to\infty}\left(1+xe^{\frac2x}\right)=\left|\begin{array}{c}x\to\infty\\ \frac2x\to0\\ e^{\frac2x}\to1\end{array}\right|=\infty\)
\(\lim\limits_{x\to-\infty}\left(1+xe^{\frac2x}\right)=\left|\begin{array}{c}x\to-\infty\\ \frac2x\to0\\ e^{\frac2x}\to1\end{array}\right|=-\infty\)
A zatem nie ma asymptot poziomych. Sprawdzamy czy będą asymptoty ukośne
\(\lim\limits_{x\to\pm\infty}\left(\frac1x+e^{\frac2x}\right)=\left|\begin{array}{c}x\to\pm\infty\\ \frac1x\to0\\ \frac2x\to0\\ e^{\frac2x}\to1\end{array}\right|=1=a\)
\(\lim\limits_{x\to\pm\infty}\left(1+xe^{\frac2x}-x\right)=\lim\limits_{x\to\pm\infty}\left(1+x\left(e^{\frac2x}-1\right)\right)=(*)\)
Teraz pomocniczo
\(\lim\limits_{x\to\pm\infty}x\left(e^{\frac2x}-1\right)=\lim\limits_{x\to\pm\infty}\frac{e^{\frac2x}-1}{\frac1x}\stackrel{H}{=}\lim\limits_{x\to\pm\infty}\frac{-\frac{2}{x^2}e^{\frac2x}}{-\frac{1}{x^2}}=2\)
skąd
\((*)=1+2=3=b\)
A zatem prosta \(y=x+3\) jest asymptotą ukośną w \(\pm\infty\)
Obliczamy dalej
\(\lim\limits_{x\to0^-}\left(1+xe^{\frac2x}\right)=\left|\begin{array}{c}x\to0^-\\ \frac2x\to-\infty\\ e^{\frac2x}\to0\end{array}\right|=1\)
\(\lim\limits_{x\to0^+}\left(1+xe^{\frac2x}\right)=\left|\begin{array}{c}x\to0^+\\ \frac2x\to\infty\\ e^{\frac2x}\to\infty\end{array}\right|=(*)\)
znowu pomocniczo
\(\lim\limits_{x\to0^+}xe^{\frac2x}=\lim\limits_{x\to0^+}\frac{e^{\frac2x}}{\frac1x}\stackrel{H}{=}\lim\limits_{x\to0^+}\frac{-\frac{2}{x^2}e^{\frac2x}}{-\frac{1}{x^2}}=\infty\)
skąd
\((*)=\infty\)
a zatem prosta \(x=0\) jest asymptotą pionową prawostronną
Pochodna, monotoniczność, ekstrema.
\(f'(x)=e^{\frac2x}-x\cdot\frac{2}{x^2}e^{\frac2x}=e^{\frac2x}\left(1-\frac2x\right)\)
\(f'(x)=0\Leftrightarrow 1-\frac2x=0\Leftrightarrow x=2\)
\(f'(x)>0\Leftrightarrow 1-\frac2x>0\Leftrightarrow x\in(-\infty,0)\cup(2,\infty)\)
\(f'(x)<0\Leftrightarrow 1-\frac2x<0\Leftrightarrow x\in(0,2)\)
Mamy zatem:
\(x\in(-\infty,0)\) - funkcja rosnąca
\(x\in(0,2)\) - funkcja malejąca
\(x\in(2,\infty)\) - funkcja rosnąca
\(x=2\) funkcja osiąga minimum równe \(f(2)=1+2e\)
Druga pochodna, wypukłość, wklęsłość, punkty przegięcia.
\(f''(x)=-\frac{2}{x^2}e^{\frac2x}\left(1-\frac2x\right)+\frac{2}{x^2}e^{\frac2x}=\frac{4}{x^3}e^{\frac2x}\)
\(f''(x)=0\) nigdy
\(f''(x)<0\Leftrightarrow x<0\) - funkcja wklęsła
\(f''(x)>0\Leftrightarrow x>0\) - funkcja wypukła
Tabela
\(\begin{array}{|c|c|c|c|c|c|}\hline
x & (-\infty,0)&0&(0,2)&2&(2,\infty)\\ \hline
f'(x) & +&\times&-&0&+\\ \hline
f''(x) & -&\times&+&+&+\\ \hline
f(x) & _{-\infty}\nearrow ^{1}&\times&^{\infty}\searrow&min&\nearrow ^{\infty} \\ \hline
\end{array}\)
(uwaga do administracji, coś interpreter \(\LaTeX-a\) nie do końca dobrze działa).
No i wykres (kliknąć aby powiększyć)
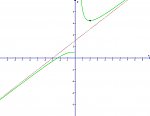
Dziedzina \(D_f=\mathbb{R}\setminus\{0\}\)
Granice na krańcach dziedziny (będą cztery)
\(\lim\limits_{x\to\infty}\left(1+xe^{\frac2x}\right)=\left|\begin{array}{c}x\to\infty\\ \frac2x\to0\\ e^{\frac2x}\to1\end{array}\right|=\infty\)
\(\lim\limits_{x\to-\infty}\left(1+xe^{\frac2x}\right)=\left|\begin{array}{c}x\to-\infty\\ \frac2x\to0\\ e^{\frac2x}\to1\end{array}\right|=-\infty\)
A zatem nie ma asymptot poziomych. Sprawdzamy czy będą asymptoty ukośne
\(\lim\limits_{x\to\pm\infty}\left(\frac1x+e^{\frac2x}\right)=\left|\begin{array}{c}x\to\pm\infty\\ \frac1x\to0\\ \frac2x\to0\\ e^{\frac2x}\to1\end{array}\right|=1=a\)
\(\lim\limits_{x\to\pm\infty}\left(1+xe^{\frac2x}-x\right)=\lim\limits_{x\to\pm\infty}\left(1+x\left(e^{\frac2x}-1\right)\right)=(*)\)
Teraz pomocniczo
\(\lim\limits_{x\to\pm\infty}x\left(e^{\frac2x}-1\right)=\lim\limits_{x\to\pm\infty}\frac{e^{\frac2x}-1}{\frac1x}\stackrel{H}{=}\lim\limits_{x\to\pm\infty}\frac{-\frac{2}{x^2}e^{\frac2x}}{-\frac{1}{x^2}}=2\)
skąd
\((*)=1+2=3=b\)
A zatem prosta \(y=x+3\) jest asymptotą ukośną w \(\pm\infty\)
Obliczamy dalej
\(\lim\limits_{x\to0^-}\left(1+xe^{\frac2x}\right)=\left|\begin{array}{c}x\to0^-\\ \frac2x\to-\infty\\ e^{\frac2x}\to0\end{array}\right|=1\)
\(\lim\limits_{x\to0^+}\left(1+xe^{\frac2x}\right)=\left|\begin{array}{c}x\to0^+\\ \frac2x\to\infty\\ e^{\frac2x}\to\infty\end{array}\right|=(*)\)
znowu pomocniczo
\(\lim\limits_{x\to0^+}xe^{\frac2x}=\lim\limits_{x\to0^+}\frac{e^{\frac2x}}{\frac1x}\stackrel{H}{=}\lim\limits_{x\to0^+}\frac{-\frac{2}{x^2}e^{\frac2x}}{-\frac{1}{x^2}}=\infty\)
skąd
\((*)=\infty\)
a zatem prosta \(x=0\) jest asymptotą pionową prawostronną
Pochodna, monotoniczność, ekstrema.
\(f'(x)=e^{\frac2x}-x\cdot\frac{2}{x^2}e^{\frac2x}=e^{\frac2x}\left(1-\frac2x\right)\)
\(f'(x)=0\Leftrightarrow 1-\frac2x=0\Leftrightarrow x=2\)
\(f'(x)>0\Leftrightarrow 1-\frac2x>0\Leftrightarrow x\in(-\infty,0)\cup(2,\infty)\)
\(f'(x)<0\Leftrightarrow 1-\frac2x<0\Leftrightarrow x\in(0,2)\)
Mamy zatem:
\(x\in(-\infty,0)\) - funkcja rosnąca
\(x\in(0,2)\) - funkcja malejąca
\(x\in(2,\infty)\) - funkcja rosnąca
\(x=2\) funkcja osiąga minimum równe \(f(2)=1+2e\)
Druga pochodna, wypukłość, wklęsłość, punkty przegięcia.
\(f''(x)=-\frac{2}{x^2}e^{\frac2x}\left(1-\frac2x\right)+\frac{2}{x^2}e^{\frac2x}=\frac{4}{x^3}e^{\frac2x}\)
\(f''(x)=0\) nigdy
\(f''(x)<0\Leftrightarrow x<0\) - funkcja wklęsła
\(f''(x)>0\Leftrightarrow x>0\) - funkcja wypukła
Tabela
\(\begin{array}{|c|c|c|c|c|c|}\hline
x & (-\infty,0)&0&(0,2)&2&(2,\infty)\\ \hline
f'(x) & +&\times&-&0&+\\ \hline
f''(x) & -&\times&+&+&+\\ \hline
f(x) & _{-\infty}\nearrow ^{1}&\times&^{\infty}\searrow&min&\nearrow ^{\infty} \\ \hline
\end{array}\)
(uwaga do administracji, coś interpreter \(\LaTeX-a\) nie do końca dobrze działa).
No i wykres (kliknąć aby powiększyć)


