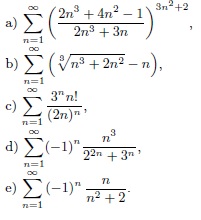Granice, pochodne, całki, szeregi
Otrzymałeś(aś) rozwiązanie do zamieszczonego zadania? - podziękuj autorowi rozwiązania! Kliknij
lukash-17
Rozkręcam się
Posty: 31 Rejestracja: 29 gru 2017, 20:35Podziękowania: 21 razy Płeć:
Post
autor: lukash-17 29 gru 2017, 20:38
Pomoże ktoś rozwiązać te zadania?
Zbadać zbieżność szeregów:
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 29 gru 2017, 21:10
trzeba przepisać , a nie wstawiać obrazki !
lukash-17
Rozkręcam się
Posty: 31 Rejestracja: 29 gru 2017, 20:35Podziękowania: 21 razy Płeć:
Post
autor: lukash-17 29 gru 2017, 21:18
Właśnie chciałem tak zrobic ale mam problem żeby to poprawnie przepisać
lukash-17
Rozkręcam się
Posty: 31 Rejestracja: 29 gru 2017, 20:35Podziękowania: 21 razy Płeć:
Post
autor: lukash-17 29 gru 2017, 21:24
a) \(\sum_{n=1}^{ \infty } \left( \frac{2n^3+4n2-1}{2n^3+3n} \right)^{3n^2+2}\)
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 29 gru 2017, 21:34
\(\displaystyle \sum_{n=1}^{ \infty } \left( \frac{2n^3+4n^2-1}{2n^3+3n} \right)^{3n^2+2}\) \(\sqrt[n]{\left( \frac{2n^3+4n^2-1}{2n^3+3n} \right)^{3n^2+2}} =\left( \frac{2n^3+4n^2-1}{2n^3+3n} \right)^{ \frac{3n^2+2}{n} } =\left( \frac{2n^3+3n+4n^2-3n-1}{2n^3+3n} \right)^{ \frac{3n^2+2}{n} } =\left(1+ \frac{4n^2-3n-1}{2n^3+3n} \right)^{ \frac{3n^2+2}{n} } =\\
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 29 gru 2017, 21:43
drugi też rozbieżny.
lukash-17
Rozkręcam się
Posty: 31 Rejestracja: 29 gru 2017, 20:35Podziękowania: 21 razy Płeć:
Post
autor: lukash-17 29 gru 2017, 21:46
b) \(\sum_{n=1}^{ \infty } \left( \sqrt[3]{n^3+2n^2} -n \right)\) \(\sum_{n=1}^{ \infty } \frac{3^nn!}{ \left(2n \right)^n }\) \(\sum_{n=1}^{ \infty } \left(-1 \right)^n \frac{n^3}{2^{2n}+3^n}\) \(\sum_{n=1}^{ \infty } \left(-1 \right)^n \frac{n}{n^2+2}\)
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 29 gru 2017, 22:05
\(\displaystyle \sum_{n=1}^{ \infty } \left( \sqrt[3]{n^3+2n^2} -n \right)\) \(\Lim_{n\to \infty } \left( \sqrt[3]{n^3+2n^2} -n \right)= \frac{2}{3} \neq 0\) - szereg nie spełnia warunku koniecznego zbieżności\(\Lim_{n\to \infty } \left( \sqrt[3]{n^3+2n^2} -n \right) \cdot \frac{ \sqrt[3]{n^3+2n^2}^2+ \sqrt[3]{n^3+2n^2} \cdot n+n^2}{ \sqrt[3]{n^3+2n^2}^2+ \sqrt[3]{n^3+2n^2} \cdot n+n^2}=\Lim_{n\to \infty } \frac{n^3+2n^2 -n^3}{ \sqrt[3]{n^3+2n^2}^2+ \sqrt[3]{n^3+2n^2} \cdot n+n^2}= \Lim_{n\to \infty } \frac{2n^2 }{ \sqrt[3]{n^3+2n^2}^2+ \sqrt[3]{n^3+2n^2} \cdot n+n^2}=\\
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 29 gru 2017, 22:25
trzeci wreszcie jest zbieżny (kryterium d'Alemberta)
lukash-17
Rozkręcam się
Posty: 31 Rejestracja: 29 gru 2017, 20:35Podziękowania: 21 razy Płeć:
Post
autor: lukash-17 29 gru 2017, 23:00
Czy ten zapis:\(\sqrt[3]{n^3+2n^2}^2\) \(\left( \sqrt[3]{n^3+2n^2}\right)^2\)
lukash-17
Rozkręcam się
Posty: 31 Rejestracja: 29 gru 2017, 20:35Podziękowania: 21 razy Płeć:
Post
autor: lukash-17 30 gru 2017, 01:03
Czy to co zrobiłem jest dobrze?\(\sum_{n=1}^{ \infty } \frac{3^nn!}{ \left(2n \right)^n }\) \(\Lim_{x\to \infty } \frac{ \frac{3^{n+1}(n+1)!}{(2n+1)^{n+1}} }{\frac{3^nn!}{ \left(2n \right)^n }}
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 30 gru 2017, 09:18
lukash-17 pisze: Czy ten zapis:\(\sqrt[3]{n^3+2n^2}^2\) \(\left( \sqrt[3]{n^3+2n^2}\right)^2\)
Tak.
radagast
Guru
Posty: 17549 Rejestracja: 09 lis 2010, 07:38Lokalizacja: WarszawaPodziękowania: 41 razy Otrzymane podziękowania: 7435 razy Płeć:
Post
autor: radagast 30 gru 2017, 09:24
lukash-17 pisze:
\(\Lim_{x\to \infty } \frac{ \frac{3^{n+1}(n+1)!}{(2n+1)^{n+1}} }{\frac{3^nn!}{ \left(2n \right)^n }}
Coś nie tak...
Policzę Ci to po Nowym Roku, a może ktoś mnie ubiegnie. Wczoraj liczyłam i wychodziła mi ta granica
\(\frac{3}{2} \cdot \frac{1}{e}\) .
Dobrego Sylwestra i szczęśliwego nowego roku