kąty

[angela128]

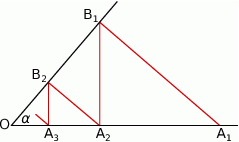
Na jednym z ramion kąta ostrego o wierzchołku O i mierze α wybrano punkty A1 ,A2 ,A3 ,... , a na drugim ramieniu punkty B1 ,B2 ,B3 ,... w ten sposób, że |OA 1| = a , AiBi ⊥ OB 1 oraz BiAi +1 ⊥ OA 1 dla wszystkich i ≥ 1 .



Wykaż, że długość nieskończonej łamanej A 1B1 A 2B 2 A3B 3... jest równa \(\frac{a}{ \tg \frac{ \alpha }{2} }\).

[Panko]

Obwód \(\Delta OB_1A_1= a+a \sin \alpha +a \cos \alpha\) i do niego się odnoszę.
Rachunek korzysta z podobieństwa kolejnych \(\Delta\) prostokątnych do powyższego \(\Delta OB_1A_1\)
Na przykładzie \(\\) \(\Delta A_1A_2B_1\)\(\sim\)\(\Delta OB_1A_1\) o co chodzi .
Zachodzi równość dla skali podobieństwa tych \(\Delta\) .
\(\frac{a \sin \alpha }{A_2A_1} = \frac{Obwód \Delta OB_1A_1 }{Obwód \Delta A_1A_2B_1}\)
Stąd mogę obliczyć sumę długości dwóch kawałków łamanej a dokładnie : \(A_1B_1+B_1A_2\)
\(Obwód \Delta A_1A_2B_1= Obwód \Delta OB_1A_1 \cdot \frac{A_2A_1}{a \sin \alpha }\)
\(A_1B_1+B_1A_2= Obwód \Delta OB_1A_1 \cdot \frac{A_2A_1}{a \sin \alpha } -A_2A_1\)
\(A_1B_1+B_1A_2= A_2A_1 \cdot ( \frac{ Obwód \Delta OB_1A_1 }{a \sin \alpha } -1)\)
\(A_1B_1+B_1A_2= A_2A_1 \cdot ( \frac{ 1+ \cos \alpha }{\sin \alpha } )\)
.........................................................................................................................
Cała łamana ( jej długość ) to \(\Lim_{n\to \infty } \frac{ 1+ \cos \alpha }{\sin \alpha } \cdot ( A_1A_2+ A_2A_3+A_3A_4+...A_nA_{n+1} )\)
Pozostaje zauważyć , że \(\Lim_{n\to \infty } ( A_1A_2+ A_2A_3+A_3A_4+...A_nA_{n+1} ) =a\)
Wtedy długość łamanej = \(\Lim_{n\to \infty } \frac{ 1+ \cos \alpha }{\sin \alpha } \cdot ( A_1A_2+ A_2A_3+A_3A_4+...A_nA_{n+1} )\) =\(\frac{ 1+ \cos \alpha }{\sin \alpha } \cdot \cdot a\)
Oraz \(\tg \frac{ \alpha }{2} = \frac{ \sin \alpha }{1+ \cos \alpha }\) i dostajemy szukany wzorek.