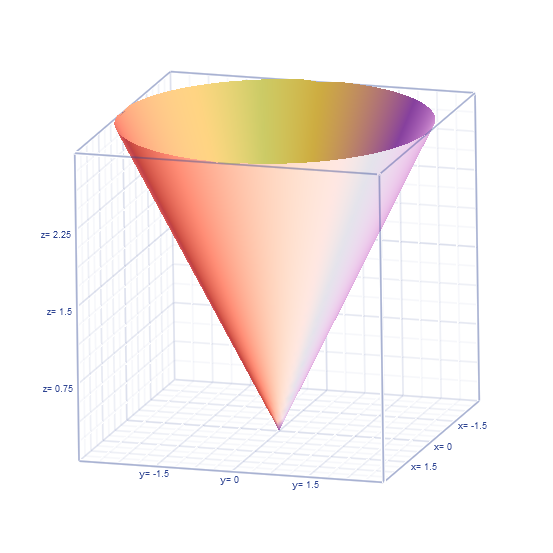
Najpierw rysunek - będzie łatwiej zrozumieć.
- graph.png (114.65 KiB) Przejrzano 2870 razy
Szukana objętość to, mówiąc obrazowo, objętość walca o podstawie takiej jak to koło widoczne na obrazku
minus objętość tego co jest pod stożkiem. Obszarem całkowania jest koło o promieniu 3.
\(V=\iint_D(3-\sqrt{x^2+y^2})dx dy\), gdzie
\(D= \left\{ (x,y)\in \rr^2: x^2+y^2\le9\right\}\)
Jeśli znasz metodę zmiany zmiennych na cylindryczne
\(\begin{cases} x=r\cos\varphi\\y=r\sin\varphi\\ |J|=r\end{cases}\) to całka stanie się dość prosta.
Teraz
\(V=\iint_{D'}(3-r)rdrd\varphi\), gdzie
\(D'= \left\{(r,\varphi): 0\le\varphi\le2\pi,\,\,\,0\le r \le 3 \right\}\)
Jak się nie pomyliłem, a ty dobrze policzysz, to wyjdzie
\(V=9\pi\)