Objętośc graniastosłupa
Otrzymałeś(aś) rozwiązanie do zamieszczonego zadania? - podziękuj autorowi rozwiązania! Kliknij
Objętośc graniastosłupa
Podstawą graniastosłupa prostego jest równoległoboku o kącie ostrym alfa. Przekątne graniastosłupa są nachylone do płaszczyzny podstawy pod kątami beta i gama (beta < gama), a wysokość graniastosłupa ma długość H. Oblicz objętość tego graniastosłupa.
- anka
- Expert

- Posty: 6587
- Rejestracja: 29 sty 2009, 23:25
- Podziękowania: 30 razy
- Otrzymane podziękowania: 1117 razy
- Płeć:
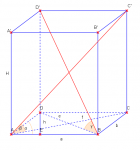
Obliczam \(e\)
\(ctg\gamma=\frac{|BD|}{|DD'|}\\
ctg\gamma=\frac{e}{H}\\
e=Hctg\gamma\)
Obliczam \(f\)
\(ctg\beta=\frac{|AC|}{|CC'|}\\
ctg\beta=\frac{f}{H}\\
f=Hctg\beta\)
Obliczam pole podstawy
\(P=ah\)
\(sin\alpha=\frac{h}{b} \Rightarrow h=b sin\alpha\)
\(P=ab sin\alpha\)
Z twierdzenia cosinusów dla trojkątów w podstawie mamy
\(e^2=a^2+b^2-2abcos\alpha \Rightarrow a^2+b^2=e^2+2abcos\alpha\)
\(f^2=a^2+b^2-2abcos(180^o-\alpha)\)
\(f^2=a^2+b^2+2abcos\alpha\)
\(f^2=e^2+2abcos\alpha+2abcos\alpha\)
\(f^2=e^2+4abcos\alpha\)
\(ab=\frac{f^2-e^2}{4cos\alpha}\)
czyli
\(P=ab sin\alpha\)
\(P=\frac{f^2-e^2}{4cos\alpha} sin\alpha\)
\(P=\frac{f^2-e^2}{4} tg\alpha\)
Podstaw
\(e=Hctg\gamma\)
\(f=Hctg\beta\)
\(V=\frac{1}{4} H^3 tg \alpha (ctg^2 \beta - ctg{^2 \gamma)\)
Znasz odpowiedź do zadania, to ją podaj. Łatwiej będzie sprawdzić czy w rozwiązaniu zadania nie ma błędu.
