Strona 1 z 1
Trapez równoramienny
: 14 kwie 2019, 17:07
autor: Ukasz12344
Który z trapezów równoramiennych opisanych na okręgu o promieniu długości r ma najmniejsze pole? Wyznacz to pole.
: 14 kwie 2019, 19:10
autor: radagast
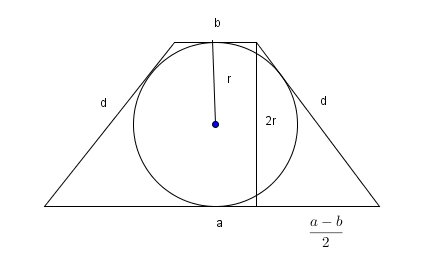
- ScreenHunter_639.jpg (8.05 KiB) Przejrzano 3245 razy
\(P(a,b)= \frac{a+b}{2} \cdot 2r=(a+b)r\)
Teraz trzeba znaleźć zależność b(a):
\(\begin{cases} a+b=2d\\ \left( \frac{a-b}{2} \right) ^2+4r^2=d^2\end{cases}\)
stąd
\(b= \frac{4r^2}{a}\)
\(P(a)= (a+ \frac{4r^2}{a})r\)
...
dalej to już standard (wychodzi, że a=2r , czyli kwadrat)
: 14 kwie 2019, 19:16
autor: Scino
radagast, właśnie kończyłem nierówną walkę z latexem i mnie wyprzedziłaś

: 14 kwie 2019, 19:24
autor: radagast
Mnie też wiele razy wyprzedzano

. Takie życie...
Re: Trapez równoramienny
: 14 kwie 2019, 20:02
autor: Panko
Można krócej
Stosując się do oznaczeń radagast pole trapezu \(P= d \cdot 2r\) czyli \(P(d)= 2r \cdot d\)
Ponieważ r jest ustalone ,to wystarczy okiełznać \(d\) .\(\)
Ponieważ , \(d^2 = 4r^2 + ( \frac{a-b}{2} )^2\) ,to \(d \ge 2r\) i minimum pola jest osiągane gdy
\(d=2r\) \(\\) i \(\\) \(\frac{a-b}{2} =0\) czyli\(\\) \(a=b= d\) .
..................................................................................................................
Taki drobiazg : aktualna VII matura próbna serwisu ( rozszerzenie , zadanie 4 ) .
Lepiej wygląda gdy brzmi ;
Wyznacz \(\\)\(m\) \(\\) aby kazda liczba całkowita spełniała nierównośc \(| 4x +m | \ge 3\)