Strona 1 z 1
Pole trapezu wpisanego w półokrąg
: 03 lis 2011, 17:32
autor: kamil13151
W półokrąg o promieniu \(R\) wpisano trapez, w którym ramię jest nachylone pod kątem \(\alpha\) do podstawy będącej średnicą okręgu. Oblicz pole trapezu.
Rysunek by się przydał.
: 03 lis 2011, 19:56
autor: radagast
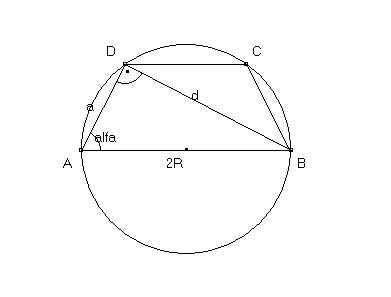
- ScreenHunter_025.jpg (8.93 KiB) Przejrzano 2940 razy
\(a=2R sin \alpha\)
\(d=2R cos \alpha\)
\(| \angle DBC|= \alpha -( \frac{ \pi }{2} -\alpha )=2 \alpha -\frac{ \pi }{2}\)
\(P_{trapezu}=P{ \Delta ABD}+P{ \Delta DBC}= \frac{1}{2}2Rasin \alpha +\frac{1}{2}adsin (2 \alpha -\frac{ \pi }{2}) =
2R^2 sin \alpha +2R^2 sin \alpha cos \alpha sin {(2 \alpha -\frac{ \pi }{2})}=
2R^2 sin \alpha -2R^2 sin \alpha cos \alpha sin {( \frac{ \pi }{2}-2 \alpha)}=
2R^2 sin \alpha -2R^2 sin \alpha cos \alpha cos {( 2 \alpha)}=
2R^2 sin \alpha(1 - cos \alpha cos {( 2 \alpha)})\)
Oczywiście o ile nie pomyliłam się w rachunkach
: 04 lis 2011, 15:02
autor: kamil13151
a skąd wniosek, że ADB to kąt prosty?
Re: Pole trapezu wpisanego w półokrąg
: 04 lis 2011, 15:40
autor: heja
Kąt wpisany oparty na średnicy jest kątem prostym.
: 04 lis 2011, 15:46
autor: kamil13151
Fakt, zastanawiam się jak to udowodnić?
: 04 lis 2011, 16:00
autor: radagast
Kąt wpisany oparty na tym samym luku , co kąt środkowy jest od niego dwa razy mniejszy
Re: Pole trapezu wpisanego w półokrąg
: 04 lis 2011, 22:15
autor: kamil13151
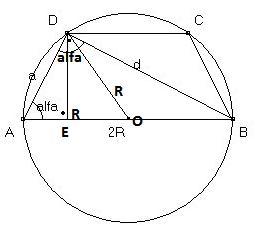
- trappp.png (12.17 KiB) Przejrzano 2907 razy
Trójkąt AOD jest równoramienny, także:
\(\frac{R}{\sin \alpha}= \frac{a}{\sin (180^{\circ}-2 \alpha)}= \frac{a}{\sin 2 \alpha}\) stąd:
\(a= \frac{R \sin 2 \alpha}{\sin \alpha} = 2R \cos \alpha\)
Teraz zajmiemy się trójkątem AED.
\(\sin \alpha= \frac{|DE|}{2R \cos \alpha} \Leftrightarrow |DE|=R \sin 2 \alpha\)
Obliczmy odcinek AE.
\(\cos \alpha = \frac{|AE|}{2R \cos \alpha} \Leftrightarrow |AE|=2R \cos^2 \alpha\)
\(|AB|=2R\)
\(|DC|=2R-2 \cdot 2R \cos^2 \alpha\)
Pole trapezu:
\(P=\frac{((|DC|+|AB|)|DE|}{2}= \frac{(2R+2R-2 \cdot 2R \cos^2 \alpha) \cdot R \sin 2 \alpha}{2}= \frac{(4R-4R \cos^2 \alpha)R 2 \sin \alpha \cos \alpha}{2}= \\ (2R-2R \cos^2 \alpha)2R \sin \alpha \cos \alpha=4R^2 \sin \alpha \cos \alpha -4R^2 \sin \alpha \cos \alpha \cos^2 \alpha=4R^2 \sin \alpha \cos \alpha (1- \cos^2 \alpha)= \\ 2R^2 \sin 2 \alpha \cdot \sin^2 \alpha\)
@radagast: źle już sam początek.
: 25 paź 2012, 19:58
autor: anetka121544
to która odpowiedź jest poprawna?
: 25 paź 2012, 20:33
autor: Galen
Ta druga odpowiedź jest bardzo dobra.
Możesz jeszcze zamienić \(sin 2\alpha\;\;na\;\;2\cdot sin\alpha\cdot cos\alpha\)
Wtedy wynik końcowy ma postać:
\(P_{ABCD}=2R^2\cdot sin^2\alpha\cdot 2\cdot sin\alpha\cdot cos\alpha=4R^2\cdot sin^3\alpha\cdot cos\alpha\)