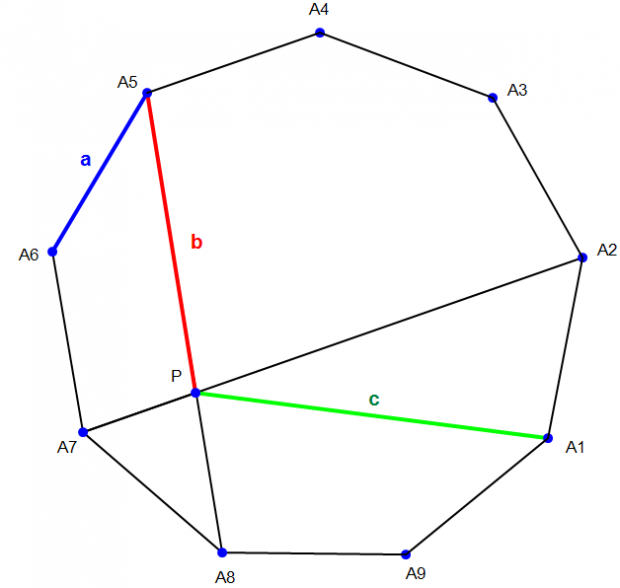
dowód w wielokącie foremnym.

[inter]

Dany jest 9−kąt foremny. Wykaż że \(a^2+b^2=c^2.\)

[Sciurius]

Ok mam dosyć szalony pomysł jak rozwiązać to zadanie:

Wierzchołki dziewięciokąta foremnego wpisanego w okrąg jednostkowy można wyznaczyć jako pierwiastki równania:

\(z^9=1\) oczywiście \(z\in \cc\) (\(\cc \) - zespolone)
gdzie \(|z|=1\)
\(z= \cos \alpha + i\sin \alpha\)
\(z^9= \cos 9\alpha + i\sin 9\alpha = 1\)
\( \begin{cases}
\cos 9\alpha = 1 \\
\sin 9\alpha =0
\end{cases} \)
\(9\alpha = 2k\pi\)
\(\alpha = \frac{2k}{9}\pi \) oczywiście \(k\in \zz\) i interesuje nas \(\alpha \in [0;2\pi]\)
Mamy więc: \(\alpha _n = \frac{2(n-1)}{9}\pi \) i \(A_n = \cos \alpha _n + i\sin \alpha _n\)
i jako że to właściwie tyle z tego co potrafie z zespolonych (myślę że da się kontynuować ten dowód w zespolonych ale niestety brak mi wiedzy) więc przejdziemy do zwykłej analitycznej oznaczając:
\(A_n = (\cos \alpha _n ;\sin \alpha _n )\) założenia co do \(\alpha _n \) się nie zmieniają

W tym miejscu warto zauważyć że mamy kilka w miarę ładnych punktów:
\(A_1 = (1;0)\)
\(A_4 = (\cos \frac{6}{9}\pi ;\sin \frac{6}{9}\pi)=(- \frac{1}{2}; \frac{ \sqrt{3} }{2} )\)
\(A_7 = (\cos \frac{12}{9}\pi ;\sin \frac{12}{9}\pi)=(- \frac{1}{2}; -\frac{ \sqrt{3} }{2} )\)

I mój pomysł w skrócie polega na tym żeby policzyć proste A5A8 i A2A7 potem punkt P i potem już z górki jest też kilka ładnych kątów np. \(60^\circ\) które można wykorzystać licząc jakąś łatwiejszą prostą i biorąc kąt między nimi

Z rzeczy wartych zauważenia to A6 jest sprzężeniem A5, A7 jest sprzężeniem A4, A8 jest sprzężeniem A3, A9 jest sprzężeniem A2 więc proste: A6A5, A7A4, A8A3, A9A2 będą prostopadłe do OX

To chyba wszystko co udało mi się jako tako wymyślić i zauważyć jak będę miał więcej determinacji to spróbuję może policzyć te proste tak czy siak trzymam kciuki że uda się popchnąć to zadanie do przodu