Strona 1 z 1
Wyznaczanie aymptot
: 13 lut 2016, 16:27
autor: Mineai
Cześć

Mam mały kłopot z wyznaczaniem asymptot. Byłąbym bardzo wdzięczna za rozwiązanie tych przykładów:
1)
\(\frac{x-1}{(lnx)^2}\)
2)
\(xarctg( \frac{x+1}{x} )\)
O ile wyznaczanie dziedzin i asymptot nawet mi idzie, tak kłopot zaczyna się przy wyznaczaniu a i b (głównie b).
Re: Wyznaczanie aymptot
: 13 lut 2016, 19:43
autor: radagast
Mineai pisze:Cześć

Mam mały kłopot z wyznaczaniem asymptot. Byłąbym bardzo wdzięczna za rozwiązanie tych przykładów:
1)
\(\frac{x-1}{(lnx)^2}\)
\(D=R_+ \bez \left\{ 1\right\}\)
\(\Lim_{x\to 0^+ } \frac{x-1}{(\ln x)^2}= \frac{-1}{- \infty } =0\) w zerze nie ma asymptoty.
\(\Lim_{x\to 1^ \pm -} \frac{x-1}{(\ln x)^2}=^H= \Lim_{x\to 1^ \pm -} \frac{x}{2\ln x} = \frac{1}{2 \cdot 0^ \pm } =\pm \infty\) asymptota pionowa obustronna x=1
\(a=\Lim_{x\to \infty } \frac{1- \frac{1}{x} }{(\ln x)^2}=0\)
\(b=\Lim_{x\to \infty } \frac{x- 1}{(\ln x)^2} =^H=\Lim_{x\to \infty } \frac{x}{2\ln x} =^H= \Lim_{x\to \infty } \frac{x}{2}= \infty\) brak asymptoty ukośnej.
: 13 lut 2016, 19:50
autor: radagast
I jeszcze obrazek potwierdzający:
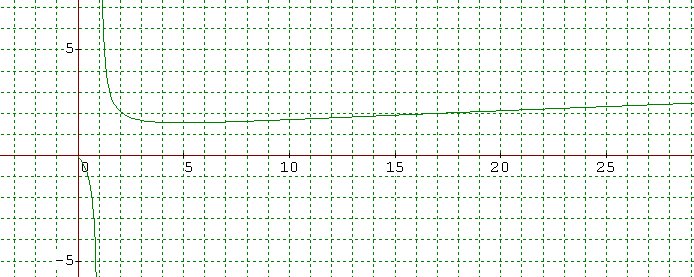
- ScreenHunter_040.jpg (71.26 KiB) Przejrzano 1611 razy
Brak asymptoty poziomej a nawet ukośnej z prawej strony jest zadziwiający ale prawdziwy .
Re: Wyznaczanie aymptot
: 13 lut 2016, 20:24
autor: radagast
Mineai pisze:Cześć

2)
\(xarctg( \frac{x+1}{x} )\)
\(D=R \bez \left\{ 0\right\}\)
\(\Lim_{x\to 0^ \pm } xarctg( \frac{x+1}{x} )=0\) -brak asymptoty pionowej
\(a=\Lim_{x\to \pm \infty } arctg( \frac{x+1}{x} )= \frac{\pi}{4}\)
\(b=\Lim_{x\to \pm \infty } xarctg( \frac{x+1}{x} )- \frac{\pi}{4}x=\Lim_{x\to \pm \infty } x(arctg( \frac{x+1}{x} )- \frac{\pi}{4})=\Lim_{x\to \pm \infty } \frac{arctg \left( \frac{x+1}{x}\right) - \frac{\pi}{4}}{ \frac{1}{x} } =^H=\Lim_{x\to \pm \infty } \frac{ \frac{1}{1+ \left( \frac{x+1}{x} \right) ^2} \cdot \left( -\frac{1}{x^2}\right) }{ -\frac{1}{x^2} }= \frac{1}{2}\)
\(y= \frac{\pi}{4} x+ \frac{1}{2}\) asymptota ukośna obustronna
: 13 lut 2016, 20:40
autor: radagast
A obrazek jest taki:
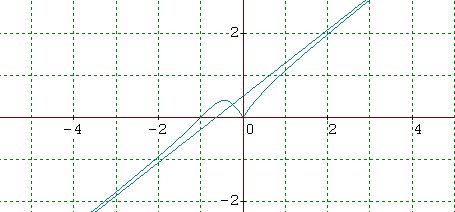
- ScreenHunter_041.jpg (22.92 KiB) Przejrzano 1595 razy
: 13 lut 2016, 20:51
autor: Mineai
Dziękuję bardzo za pomoc

Mam jeszcze jeden problem odnośnie czegoś ciut innego, a dokładniej chodzi mi o ekstrema w takiej funkcji:
\(3( \sqrt[3]{(x-1)^2})e^x\)
: 13 lut 2016, 21:07
autor: radagast
exteremum jest w 1 (minimum) i w \(\frac{1}{3}\) (maximum). Liczy się dość łatwo. Z czym problem ?
: 13 lut 2016, 21:13
autor: Mineai
Głównie z pochodną. Raz liczyłam i wyszło \(3e^x\), innym razem trójka się skróciła (ale po przyrównaniu do zera nadal wyjdzie na to samo), a podejrzewam że wynik jest jeszcze zupełnie inny.
Re:
: 14 lut 2016, 06:34
autor: Binio1
Mineai pisze:
\(3( \sqrt[3]{(x-1)^2})e^x\)
\(f(x) = 3(x^2-2x+1)^\frac{1}{3}e^x\)
\(f'(x) = 3[((x^2-2x+1)^{\frac{1}{3}})'(e^x)+((x^2-2x+1)^{\frac{1}{3}})(e^x)'] =\)
\(= 3[\frac{1}{3}\frac{1}{(x^2-2x+1)^\frac{2}{3}}(x^2-2x+1)'(e^x) + ((x^2-2x+1)^\frac{1}{3})(e^x)] =\)
\(= 3[\frac{e^x(2x-2)}{3((x-1)^2)^{\frac{2}{3}}} + ((x-1)^2)^\frac{1}{3}(e^x)] =\)
\(= 3[\frac{2xe^x-2e^x}{3((x-1)^2)^{\frac{2}{3}}} + \frac{3(x-1)^{\frac{4}{3}}e^x(x-1)^{\frac{2}{3}}}{3((x-1)^2)^{\frac{2}{3}}}] =\)
\(= \frac{2xe^x-2e^x+3e^x(x-1)^2}{((x-1)^2)^\frac{2}{3}} = \frac{e^x(2x-2+3x^2-6x+3)}{(x-1)^\frac{4}{3}} =\)
\(= \frac{e^x(3x^2-4x+1)}{(x-1)^\frac{4}{3}}\)
Pochodna bedzie rowna 0 gdy:
\(3x^2-4x+1 = 0\)
\(\Delta = 16 - 12 = 4\)
\(x_{1} = \frac{4-2}{6} = \frac{1}{3}\)
\(x_{2} = \frac{4+2}{6} = 1\)
Re: Re:
: 14 lut 2016, 10:44
autor: radagast
Binio1 pisze:
Pochodna bedzie rowna 0 gdy:
\(3x^2-4x+1 = 0\)
\(\Delta = 16 - 12 = 4\)
\(x_{1} = \frac{4-2}{6} = \frac{1}{3}\)
\(x_{2} = \frac{4+2}{6} = 1\)
Nie za bardzo... W 0 nie ma pochodnej

(ale minimum jest

)
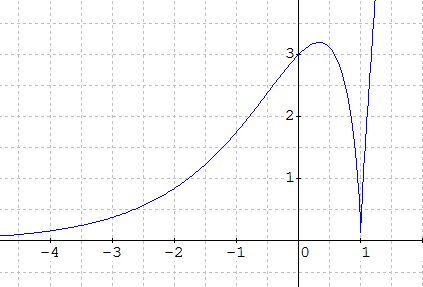
- ScreenHunter_1055.jpg (23.58 KiB) Przejrzano 1530 razy
